初中数学频数（率）分布表试题

近几年，国内快递业务快速发展，由于其便捷、高效，人们越来越多地通过快递公司代办点来代寄包裹．某快递公司某地区一代办点对60天中每天代寄的包裹数与天数的数据（每天代寄包裹数、天数均为整数）统计如下：

（1）求该数据中每天代寄包裹数在范围内的天数；

（2）若该代办点对顾客代寄包裹的收费标准为：重量小于或等于1千克的包裹收费8元；重量超1千克的包裹，在收费8元的基础上，每超过1千克（不足1千克的按1千克计算）需再收取2元．

①某顾客到该代办点寄重量为1.6千克的包裹，求该顾客应付多少元费用？

②这60天中，该代办点为顾客代寄的包裹中有一部分重量超过2千克，且不超过5千克．现从中随机抽取40件包裹的重量数据作为样本，统计如下：

重量（单位：千克）
件数（单位：件）	15	10	15

求这40件包裹收取费用的平均数．

某校为了解七年级学生的身体素质情况，从七年级各班随机抽取了数量相同的男生和女生，组成一个容量为60的样本，进行各项体育项目的测试．下表是通过整理样本数据，得到的关于每个个体测试成绩的部分统计表：

某校60名学生体育测试成绩频数分布表

成绩	划记	频数	百分比
优秀		$a$	$30\%$
良好		30	$b$
合格		9	$15\%$
不合格		3	$5\%$
合计	60	60	$100\%$

如果该校七年级共有300名学生，根据以上数据，估计该校七年级学生身体素质良好及以上的人数为 　　人．

某批彩色弹力球的质量检验结果如下表：

抽取的彩色弹力球数 $n$	500	1000	1500	2000	2500
优等品频数 $m$	471	946	1426	1898	2370
优等品频率 $\frac{m}{n}$	0.942	0.946	0.951	0.949	0.948

（1）请在图中完成这批彩色弹力球“优等品”频率的折线统计图

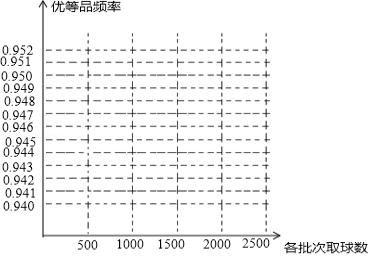
（2）这批彩色弹力球“优等品”概率的估计值大约是多少？（精确到0.01）

（3）从这批彩色弹力球中选择5个黄球、13个黑球、22个红球，它们除了颜色外都相同，将它们放入一个不透明的袋子中，求从袋子中摸出一个球是黄球的概率．

（4）现从第（3）问所说的袋子中取出若干个黑球，并放入相同数量的黄球，搅拌均匀，使从袋子中摸出一个黄球的概率为 $\frac{1}{4}$，求取出了多少个黑球？

某校为了解学生课外阅读时间情况，随机抽取了 $m$ 名学生，根据平均每天课外阅读时间的长短，将他们分为 $A$ ， $B$ ， $C$ ， $D$ 四个组别，并绘制了如图不完整的频数分布表和扇形统计图．

频数分布表

组别	时间 $/$ （小时）	频 $/$ 人数
$A$	$0⩽t<0.5$	$2n$
$B$	$0⩽t<1$	20
$C$	$1⩽t<1.5$	$n+10$
$D$	$t⩾1.5$	5

请根据图表中的信息解答下列问题：

（1）求 $m$ 与 $n$ 的值，并补全扇形统计图；

（2）直接写出所抽取的 $m$ 名学生平均每天课外阅读时间的中位数落在的组别；

（3）该校现有1500名学生，请你估计该校有多少名学生平均每天课外阅读时间不少于1小时．

某市举行“传承好家风”征文比赛，已知每篇参赛征文成绩记 $m$分 $(60⩽m⩽100)$，组委会从1000篇征文中随机抽取了部分参赛征文，统计了它们的成绩，并绘制了如图不完整的两幅统计图表．

征文比赛成绩频数分布表

分数段	频数	频率
$60⩽m<70$	38	0.38
$70⩽m<80$	$a$	0.32
$80⩽m<90$	$b$	$c$
$90⩽m⩽100$	10	0.1
合计		1

请根据以上信息，解决下列问题：

（1）征文比赛成绩频数分布表中 $c$的值是　　；

（2）补全征文比赛成绩频数分布直方图；

（3）若80分以上（含80分）的征文将被评为一等奖，试估计全市获得一等奖征文的篇数．

在"尚科学，爱运动"主题活动中，某校在七年级学生中随机抽取部分同学就"一分钟跳绳"进行测试，并将测试成绩 $x$ （单位：次）进行整理后分成六个等级，分别用 $A$ ， $B$ ， $C$ ， $D$ ， $E$ ， $F$ 表示，并绘制成如图所示的两幅不完整的统计图表．请根据图表中所给出的信息解答下列问题：

组别	成绩     $x$ （单位：次）	人数
$A$	$70⩽x<90$	4
$B$	$90⩽x<110$	15
$C$	$110⩽x<130$	18
$D$	$130⩽x<150$	12
$E$	$150⩽x<170$	$m$
$F$	$170⩽x<190$	5

（1）本次测试随机抽取的人数是 　 　人， $m=$ 　　；

（2）求 $C$ 等级所在扇形的圆心角的度数；

（3）若该校七年级学生共有300人，且规定不低于130次的成绩为优秀，请你估计该校七年级学生中有多少人能够达到优秀．

在太空种子种植体验实践活动中，为了解"宇番2号"番茄，某校科技小组随机调查60株番茄的挂果数量 $x$ （单位：个），并绘制如下不完整的统计图表：

"宇番2号"番茄挂果数量统计表

挂果数量     $x$ （个）	频数（株）	频率
$25⩽x<35$	6	0.1
$35⩽x<45$	12	0.2
$45⩽x<55$	$a$	0.25
$55⩽x<65$	18	$b$
$65⩽x<75$	9	0.15

请结合图表中的信息解答下列问题：

（1）统计表中， $a=$ 　      　， $b=$ 　      　；

（2）将频数分布直方图补充完整；

（3）若绘制"番茄挂果数量扇形统计图"，则挂果数量在" $35⩽x<45$ "所对应扇形的圆心角度数为 　     　 $°$ ；

（4）若所种植的"宇番2号"番茄有1000株，则可以估计挂果数量在" $55⩽x<65$ "范围的番茄有 　      　株．

为加强安全教育，某校开展了"防溺水"安全知识竞赛，想了解七年级学生对"防溺水"安全知识的掌握情况，现从七年级学生中随机抽取50名学生进行竞赛，并将他们的竞赛成绩（百分制）进行整理、描述和解析．部分信息如下：

$a$ ．七年级参赛学生成绩频数分布直方图（数据分成五组： $50⩽x<60$ ， $60⩽x<70$ ， $70⩽x<80$ ， $80⩽x<90$ ， $90⩽x⩽100)$ 如图所示

$b$ ．七年级参赛学生成绩在 $70⩽x<80$ 这一组的具体得分是：70   71   73   75   76   76   76   77   77   78   79

$c$ ．七年级参赛学生成绩的平均数、中位数、众数如下：

年级	平均数	中位数	众数
七	76.9	$m$	80

$d$ ．七年级参赛学生甲的竞赛成绩得分为79分．

根据以上信息，回答下列问题：

（1）在这次测试中，七年级在75分以上（含75分）的有 　 　人；

（2）表中 $m$ 的值为 　　；

（3）在这次测试中，七年级参赛学生甲的竞赛成绩得分排名年级第 　　名；

（4）该校七年级学生有500人，假设全部参加此次测试，请估计七年级成绩超过平均数76.9分的人数．

为了了解现行简化汉字的笔画画数情况，某同学随机选取语文课本的一篇文章，对其部分文字的笔画数进行统计，结果如下表：

笔画数	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15
字数	4	8	10	16	14	20	24	36	16	14	11	9	10	7	1

请答案下列问题：

（1）被统计汉字笔画数的众数是多少？

（2）该同学将数据进行整理，按如下方案分组统计，并制作扇形统计图：

分组	笔画数 $x$ （画 $)$	$A$ 字数（个 $)$
$A$ 组	$1⩽x⩽3$	22
$B$ 组	$4⩽x⩽6$	$m$
$C$ 组	$7⩽x⩽9$	76
$D$ 组	$10⩽x⩽12$	$n$
$E$ 组	$13⩽x⩽15$	18

请确定上表中的 $m$ 、 $n$ 的值及扇形统计图中 $B$ 组对应扇形圆心角的度数；

（3）若这篇文章共有3500个汉字，估计笔画数在 $7~9$ 画 $(C$ 组）的字数有多少个？

为增强学生垃圾分类意识，推动垃圾分类进校园．某初中学校组织全校1200名学生参加了"垃圾分类知识竞赛"，为了解学生的答题情况，学校考虑采用简单随机抽样的方法抽取部分学生的成绩进行调查分析．

（1）学校设计了以下三种抽样调查方案：

方案一：从初一、初二、初三年级中指定部分学生成绩作为样本进行调查分析；

方案二：从初一、初二年级中随机抽取部分男生成绩及在初三年级中随机抽取部分女生成绩进行调查分析；

方案三：从三个年级全体学生中随机抽取部分学生成绩进行调查分析．

其中抽取的样本具有代表性的方案是 　    　．（填"方案一"、"方案二"或"方案三" $)$

（2）学校根据样本数据，绘制成下表 $(90$ 分及以上为"优秀"，60分及以上为"及格" $):$

样本容量	平均分	及格率	优秀率	最高分	最低分
100	93.5	$100\%$	$70\%$	100	80
分数段统计（学生成绩记为 $x)$
分数段	$0⩽x<80$	$80⩽x<85$	$85⩽x<90$	$90⩽x<95$	$95⩽x⩽100$
频数	0	5	25	30	40

请结合表中信息解答下列问题：

①估计该校1200名学生竞赛成绩的中位数落在哪个分数段内；

②估计该校1200名学生中达到"优秀"的学生总人数．

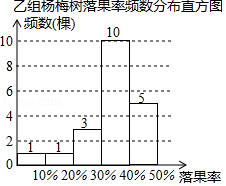
杨梅果实成熟期正值梅雨季节，雨水过量会导致杨梅树大量落果，给果农造成损失．为此，市农科所开展了用防雨布保护杨梅果实的实验研究．在某杨梅果园随机选择40棵杨梅树，其中20棵加装防雨布（甲组），另外20棵不加装防雨布（乙组）．在杨梅成熟期，统计了甲、乙两组中每一棵杨梅树的落果率（落地的杨梅颗数占树上原有杨梅颗数的百分比），绘制成统计图表（数据分组包含左端值不包含右端值）．

甲组杨梅树落果率频数分布表

落果率	组中值	频数（棵     $)$
$0⩽x<10\%$	$5\%$	12
$10\%⩽x<20\%$	$15\%$	4
$20\%⩽x<30\%$	$25\%$	2
$30\%⩽x<40\%$	$35\%$	1
$40\%⩽x<50\%$	$45\%$	1

（1）甲、乙两组分别有几棵杨梅树的落果率低于 $20\%$ ？

（2）请用落果率的中位数或平均数，评价市农科所"用防雨布保护杨梅果实"的实际效果；

（3）若该果园的杨梅树全部加装这种防雨布，落果率可降低多少？说出你的推断依据．

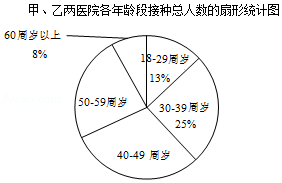
“此生无悔入华夏，来世再做中国人！”自疫情暴发以来，我国科研团队经过不懈努力，成功地研发出了多种“新冠”疫苗，并在全国范围内免费接种．截止2021年5月18日 $16:20$，全球接种“新冠”疫苗的比例为 $18.29\%$；中国累计接种4.2亿剂，占全国人口的 $29.32\%$．以下是某地甲、乙两家医院5月份某天各年龄段接种疫苗人数的频数分布表和接种总人数的扇形统计图：

	甲医院			乙医院
年龄段	频数	频率	频数		频率
$18-29$周岁	900	0.15	400		0.1
$30-39$周岁	$a$	0.25	1000		0.25
$40-49$周岁	2100	$b$	$c$		0.225
$50-59$周岁	1200	0.2	1200		0.3
60周岁以上	300	0.05	500		0.125

（1）根据上面图表信息，回答下列问题：

①填空： $a=$　　， $b=$　　， $c=$　　；

②在甲、乙两医院当天接种疫苗的所有人员中， $40-49$周岁年龄段人数在扇形统计图中所占圆心角为 　　；

（2）若 $A$、 $B$、 $C$三人都于当天随机到这两家医院接种疫苗，求这三人在同一家医院接种的概率．

为发展乡村经济，某村根据本地特色，创办了山药粉加工厂．该厂需购置一台分装机，计划从商家推荐试用的甲、乙两台不同品牌的分装机中选择．试用时，设定分装的标准质量为每袋 $500g$，与之相差大于 $10g$为不合格．为检验分装效果，工厂对这两台机器分装的成品进行了抽样和分析，过程如下：

$[$收集数据 $]$从甲、乙两台机器分装的成品中各随机抽取20袋，测得实际质量（单位： $g)$如下：

甲：501    497   498    502    513   489   506   490   505   486

      502    503   498    497    491   500   505   502   504   505

乙：505   499   502    491    487   506   493   505   499   498

      502    503   501    490    501   502   511   499   499    501

$[$整理数据 $]$整理以上数据，得到每袋质量 $x\left(g\right)$的频数分布表．

质量 频数 机器	$485⩽x<490$	$490⩽x<495$	$495⩽x<500$	$500⩽x<505$	$505⩽x<510$	$510⩽x<515$
甲	2	2	4	7	4	1
乙	1	3	5	7	3	1

$[$分析数据 $]$根据以上数据，得到以下统计量．

统计量 机器	平均数	中位数	方差	不合格率
甲	499.7	501.5	42.01	$b$
乙	499.7	$a$	31.81	$10\%$

根据以上信息，回答下列问题：

（1）表格中的 $a=$　　， $b=$　　；

（2）综合上表中的统计量，判断工厂应选购哪一台分装机，并说明理由．

现今“微信运动”被越来越多的人关注和喜爱，某兴趣小组随机调查了我市50名教师某日“微信运动”中的步数情况进行统计整理，绘制了如下的统计图表（不完整） $:$

步数	频数	频率
$0⩽x<4000$	8	$a$
$4000⩽x<8000$	15	0.3
$8000⩽x<12000$	12	$b$
$12000⩽x<16000$	$c$	0.2
$16000⩽x<20000$	3	0.06
$20000⩽x<24000$	$d$	0.04

请根据以上信息，解答下列问题：

（1）写出 $a$， $b$， $c$， $d$的值并补全频数分布直方图；

（2）本市约有37800名教师，用调查的样本数据估计日行走步数超过12000步（包含12000步）的教师有多少名？

（3）若在50名被调查的教师中，选取日行走步数超过16000步（包含16000步）的两名教师与大家分享心得，求被选取的两名教师恰好都在20000步（包含20000步）以上的概率．

某学校为调查学生的兴趣爱好，抽查了部分学生，并制作了如下表格与条形统计图：

	频数	频率
体育	40	0.4
科技	25	a
艺术	b	0.15
其它	20	0.2

请根据上图完成下面题目：

（1）总人数为 　　人， a＝ 　　， b＝ 　　．

（2）请你补全条形统计图．

（3）若全校有600人，请你估算一下全校喜欢艺术类学生的人数有多少？