初中数学频数（率）分布表试题

某中学抽取了40名学生参加"平均每周课外阅读时间"的调查，由调查结果绘制了如下不完整的频数分布表和扇形统计图．

频数分布表

组别	时间/小时	频数/人数
A组	0≤ t＜1	2
B组	1≤ t＜2	m
C组	2≤ t＜3	10
D组	3≤ t＜4	12
E组	4≤ t＜5	7
F组	t≥5	4

请根据图表中的信息解答下列问题：

（1）求频数分布表中 m的值；

（2）求 B组， C组在扇形统计图中分别对应扇形的圆心角度数，并补全扇形统计图；

（3）已知 F组的学生中，只有1名男生，其余都是女生，用列举法求以下事件的概率：从 F组中随机选取2名学生，恰好都是女生．

阅读对学生的成长有着深远的影响，某中学为了解学生每周课余阅读的时间，在本校随机抽取了若干名学生进行调查，并依据调查结果绘制了以下不完整的统计图表．

组别	时间（小时）	频数（人数）	频率
$A$	$0⩽t⩽0.5$	6	0.15
$B$	$0.5⩽t⩽1$	$a$	0.3
$C$	$1⩽t⩽1.5$	10	0.25
$D$	$1.5⩽t⩽2$	8	$b$
$E$	$2⩽t⩽2.5$	4	0.1
合计			1

请根据图表中的信息，解答下列问题：

（1）表中的 $a=$　        　， $b=$　       　，中位数落在　     　组，将频数分布直方图补全；

（2）估计该校2000名学生中，每周课余阅读时间不足0.5小时的学生大约有多少名？

（3） $E$组的4人中，有1名男生和3名女生，该校计划在 $E$组学生中随机选出两人向全校同学作读书心得报告，请用画树状图或列表法求抽取的两名学生刚好是1名男生和1名女生的概率．

为了弘扬荆州优秀传统文化，某中学举办了荆州文化知识大赛，其规则是：每位参赛选手回答100道选择题，答对一题得1分，不答或错答不得分、不扣分，赛后对全体参赛选手的答题情况进行了相关统计，整理并绘制成如下图表：

组别	分数段	频数（人）	频率
1	50≤x＜60	30	0.1
2	60≤x＜70	45	0.15
3	70≤x＜80	60	n
4	80≤x＜90	m	0.4
5	90≤x＜100	45	0.15

请根据以图表信息，解答下列问题：

（1）表中m＝　　，n＝　 　；

（2）补全频数分布直方图；

（3）全体参赛选手成绩的中位数落在第几组；

（4）若得分在80分以上（含80分）的选手可获奖，记者从所有参赛选手中随机采访1人，求这名选手恰好是获奖者的概率．

某鞋店在一周内销售某款女鞋，尺码（单位： $\mathit{cm})$数据收集如下：

24	23.5	21.5	23.5	24.5	23	22	23.5	23.5	23	22.5	23.5	23.5	22.5	24
24	22.5	25	23	23	23.5	23	22.5	23	23.5	23.5	23	24	22	22.5

绘制如图不完整的频数分布表及频数分布直方图：

尺码 $/\mathit{cm}$	划记	频数
$21.5⩽x<22.5$		3
$22.5⩽x<23.5$
$23.5⩽x<24.5$		13
$24.5⩽x<25.5$		2

（1）请补全频数分布表和频数分布直方图；

（2）若店主要进货，她最应该关注的是尺码的众数，上面数据的众数为　　；

（3）若店主下周对该款女鞋进货120双，尺码在 $23.5⩽x<25.5$范围的鞋应购进约多少双？

为了解某市初三学生的体育测试成绩和课外体育锻炼时间的情况，现从全市初三学生体育测试成绩中随机抽取200名学生的体育测试成绩作为样本．体育成绩分为四个等次：优秀、良好、及格、不及格．

体育锻炼时间	人数
4≤x≤6
2≤x＜4	43
0≤x＜2	15

（1）试求样本扇形图中体育成绩“良好”所对扇形圆心角的度数；

（2）统计样本中体育成绩“优秀”和“良好”学生课外体育锻炼时间表（如图表所示），请将图表填写完整（记学生课外体育锻炼时间为x小时）；

（3）全市初三学生中有14400人的体育测试成绩为“优秀”和“良好”，请估计这些学生中课外体育锻炼时间不少于4小时的学生人数．

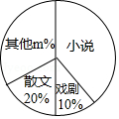
九年级一班开展了“读一本好书”的活动，班委会对学生阅读书籍的情况进行了问卷调查，问卷设置了“小说”“戏剧”“散文”“其他”四个选项，每位同学仅选一项，根据调查结果绘制了如下不完整的频数分布表和扇形统计图．

类别	频数（人数）	频率
小说	16
戏剧	4
散文	$a$
其他	$b$
合计		1

根据图表提供的信息，解答下列问题：

（1）直接写出 $a$， $b$， $m$的值；

（2）在调查问卷中，甲、乙、丙、丁四位同学选择了“戏剧”类，现从以上四位同学中任意选出2名同学参加学校的戏剧兴趣小组，请用列表法或画树状图的方法，求选取的2人恰好是乙和丙的概率．

某校在践行“社会主义核心价值观”演讲比赛中，对名列前20名的选手的综合分数m进行分组统计，结果如表所示：

组号	分组	频数
一	6≤m＜7	2
二	7≤m＜8	7
三	8≤m＜9	a
四	9≤m≤10	2

（1）求a的值；

（2）若用扇形图来描述，求分数在8≤m＜9内所对应的扇形图的圆心角大小；

（3）将在第一组内的两名选手记为：A₁、A₂，在第四组内的两名选手记为：B₁、B₂，从第一组和第四组中随机选取2名选手进行调研座谈，求第一组至少有1名选手被选中的概率（用树状图或列表法列出所有可能结果）．

某校为了解七年级学生的身体素质情况，从七年级各班随机抽取了数量相同的男生和女生，组成一个容量为60的样本，进行各项体育项目的测试．下表是通过整理样本数据，得到的关于每个个体测试成绩的部分统计表：

某校60名学生体育测试成绩频数分布表

成绩	划记	频数	百分比
优秀		$a$	$30\%$
良好		30	$b$
合格		9	$15\%$
不合格		3	$5\%$
合计	60	60	$100\%$

如果该校七年级共有300名学生，根据以上数据，估计该校七年级学生身体素质良好及以上的人数为 　　人．

"学而时习之，不亦说乎？"古人把经常复习当作是一种乐趣．某校为了解九年级（一 $)$ 班学生每周的复习情况，班长对该班学生每周的复习时间进行了调查，复习时间四舍五入后只有4种：1小时，2小时，3小时，4小时，已知该班共有50人，根据调查结果，制作了两幅不完整的统计图表，该班女生一周的复习时间数据（单位：小时）如下：

1，1，1，2，2，2，2，2，2，2，3，3，3，3，4，4，4，4，4，4

九年级（一 $)$ 班女生一周复习时间频数分布表

复习时间	频数（学生人数）
1小时	3
2小时	$a$
3小时	4
4小时	6

（1）统计表中 $a=$ 　　，该班女生一周复习时间的中位数为 　　小时；

（2）扇形统计图中，该班男生一周复习时间为4小时所对应圆心角的度数为 　　 $°$ ；

（3）该校九年级共有600名学生，通过计算估计一周复习时间为4小时的学生有多少名？

（4）在该班复习时间为4小时的女生中，选择其中四名分别记为 $A$ ， $B$ ， $C$ ， $D$ ，为了培养更多学生对复习的兴趣，随机从该四名女生中选取两名进行班会演讲，请用树状图或者列表法求恰好选中 $B$ 和 $D$ 的概率．

深圳市某学校抽样调查， 类学生骑共享单车， 类学生坐公交车、私家车等， 类学生步行， 类学生（其它），根据调查结果绘制了不完整的统计图．

类型	频数	频率
	30
	18	0.15
		0.40

（1）学生共 　　人， 　 　， 　 　；

（2）补全条形统计图；

（3）若该校共有2000人，骑共享单车的有 　 　人．

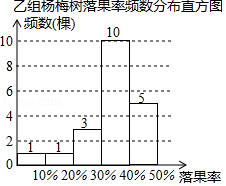
杨梅果实成熟期正值梅雨季节，雨水过量会导致杨梅树大量落果，给果农造成损失．为此，市农科所开展了用防雨布保护杨梅果实的实验研究．在某杨梅果园随机选择40棵杨梅树，其中20棵加装防雨布（甲组），另外20棵不加装防雨布（乙组）．在杨梅成熟期，统计了甲、乙两组中每一棵杨梅树的落果率（落地的杨梅颗数占树上原有杨梅颗数的百分比），绘制成统计图表（数据分组包含左端值不包含右端值）．

甲组杨梅树落果率频数分布表

落果率	组中值	频数（棵     $)$
$0⩽x<10\%$	$5\%$	12
$10\%⩽x<20\%$	$15\%$	4
$20\%⩽x<30\%$	$25\%$	2
$30\%⩽x<40\%$	$35\%$	1
$40\%⩽x<50\%$	$45\%$	1

（1）甲、乙两组分别有几棵杨梅树的落果率低于 $20\%$ ？

（2）请用落果率的中位数或平均数，评价市农科所"用防雨布保护杨梅果实"的实际效果；

（3）若该果园的杨梅树全部加装这种防雨布，落果率可降低多少？说出你的推断依据．

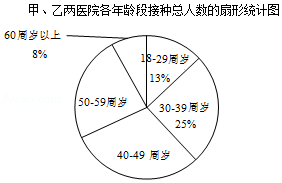
“此生无悔入华夏，来世再做中国人！”自疫情暴发以来，我国科研团队经过不懈努力，成功地研发出了多种“新冠”疫苗，并在全国范围内免费接种．截止2021年5月18日 $16:20$，全球接种“新冠”疫苗的比例为 $18.29\%$；中国累计接种4.2亿剂，占全国人口的 $29.32\%$．以下是某地甲、乙两家医院5月份某天各年龄段接种疫苗人数的频数分布表和接种总人数的扇形统计图：

	甲医院			乙医院
年龄段	频数	频率	频数		频率
$18-29$周岁	900	0.15	400		0.1
$30-39$周岁	$a$	0.25	1000		0.25
$40-49$周岁	2100	$b$	$c$		0.225
$50-59$周岁	1200	0.2	1200		0.3
60周岁以上	300	0.05	500		0.125

（1）根据上面图表信息，回答下列问题：

①填空： $a=$　　， $b=$　　， $c=$　　；

②在甲、乙两医院当天接种疫苗的所有人员中， $40-49$周岁年龄段人数在扇形统计图中所占圆心角为 　　；

（2）若 $A$、 $B$、 $C$三人都于当天随机到这两家医院接种疫苗，求这三人在同一家医院接种的概率．

为发展乡村经济，某村根据本地特色，创办了山药粉加工厂．该厂需购置一台分装机，计划从商家推荐试用的甲、乙两台不同品牌的分装机中选择．试用时，设定分装的标准质量为每袋 $500g$，与之相差大于 $10g$为不合格．为检验分装效果，工厂对这两台机器分装的成品进行了抽样和分析，过程如下：

$[$收集数据 $]$从甲、乙两台机器分装的成品中各随机抽取20袋，测得实际质量（单位： $g)$如下：

甲：501    497   498    502    513   489   506   490   505   486

      502    503   498    497    491   500   505   502   504   505

乙：505   499   502    491    487   506   493   505   499   498

      502    503   501    490    501   502   511   499   499    501

$[$整理数据 $]$整理以上数据，得到每袋质量 $x\left(g\right)$的频数分布表．

质量 频数 机器	$485⩽x<490$	$490⩽x<495$	$495⩽x<500$	$500⩽x<505$	$505⩽x<510$	$510⩽x<515$
甲	2	2	4	7	4	1
乙	1	3	5	7	3	1

$[$分析数据 $]$根据以上数据，得到以下统计量．

统计量 机器	平均数	中位数	方差	不合格率
甲	499.7	501.5	42.01	$b$
乙	499.7	$a$	31.81	$10\%$

根据以上信息，回答下列问题：

（1）表格中的 $a=$　　， $b=$　　；

（2）综合上表中的统计量，判断工厂应选购哪一台分装机，并说明理由．

现今“微信运动”被越来越多的人关注和喜爱，某兴趣小组随机调查了我市50名教师某日“微信运动”中的步数情况进行统计整理，绘制了如下的统计图表（不完整） $:$

步数	频数	频率
$0⩽x<4000$	8	$a$
$4000⩽x<8000$	15	0.3
$8000⩽x<12000$	12	$b$
$12000⩽x<16000$	$c$	0.2
$16000⩽x<20000$	3	0.06
$20000⩽x<24000$	$d$	0.04

请根据以上信息，解答下列问题：

（1）写出 $a$， $b$， $c$， $d$的值并补全频数分布直方图；

（2）本市约有37800名教师，用调查的样本数据估计日行走步数超过12000步（包含12000步）的教师有多少名？

（3）若在50名被调查的教师中，选取日行走步数超过16000步（包含16000步）的两名教师与大家分享心得，求被选取的两名教师恰好都在20000步（包含20000步）以上的概率．

某学校为调查学生的兴趣爱好，抽查了部分学生，并制作了如下表格与条形统计图：

	频数	频率
体育	40	0.4
科技	25	a
艺术	b	0.15
其它	20	0.2

请根据上图完成下面题目：

（1）总人数为 　　人， a＝ 　　， b＝ 　　．

（2）请你补全条形统计图．

（3）若全校有600人，请你估算一下全校喜欢艺术类学生的人数有多少？