初中数学解直角三角形的应用-仰角俯角问题填空题

如图，某城市的电视塔 $\mathit{AB}$坐落在湖边，数学老师带领学生隔湖测量电视塔 $\mathit{AB}$的高度，在点 $M$处测得塔尖点 $A$的仰角 $\angle \mathit{AMB}$为 $22.5°$，沿射线 $\mathit{MB}$方向前进200米到达湖边点 $N$处，测得塔尖点 $A$在湖中的倒影 $A\text{'}$的俯角 $\angle A\text{'}\mathit{NB}$为 $45°$，则电视塔 $\mathit{AB}$的高度为　　米（结果保留根号）．

如图，建筑物 $C$上有一杆 $\mathit{AB}$．从与 $\mathit{BC}$相距 $10m$的 $D$处观测旗杆顶部 $A$的仰角为 $53°$，观测旗杆底部 $B$的仰角为 $45°$，则旗杆 $\mathit{AB}$的高度约为　　 $m$（结果取整数，参考数据： $\sin 53°\approx 0.80$， $\cos 53°\approx 0.60$， $\tan 53°\approx 1.33)$．

如图，某景区的两个景点 $A$、 $B$处于同一水平地面上、一架无人机在空中沿 $\mathit{MN}$方向水平飞行进行航拍作业， $\mathit{MN}$与 $\mathit{AB}$在同一铅直平面内，当无人机飞行至 $C$处时、测得景点 $A$的俯角为 $45°$，景点 $B$的俯角为 $30°$，此时 $C$到地面的距离 $\mathit{CD}$为100米，则两景点 $A$、 $B$间的距离为　　米（结果保留根号）．

如图，在点 $B$处测得塔顶 $A$的仰角为 $30°$，点 $B$到塔底 $C$的水平距离 $\mathit{BC}$是 $30m$，那么塔 $\mathit{AC}$的高度为　　 $m$（结果保留根号）．

如图，小明为了测量校园里旗杆 $\mathit{AB}$的高度，将测角仪 $\mathit{CD}$竖直放在距旗杆底部 $B$点 $6m$的位置，在 $D$处测得旗杆顶端 $A$的仰角为 $53°$，若测角仪的高度是 $1.5m$，则旗杆 $\mathit{AB}$的高度约为　　 $m$．（精确到 $0.1m$．参考数据： $\sin 53°\approx 0.80$， $\cos 53°\approx 0.60$， $\tan 53°\approx 1.33)$

如图所示，运载火箭从地面 $L$处垂直向上发射，当火箭到达 $A$点时，从位于地面 $R$处的雷达测得 $\mathit{AR}$的距离是 $40\mathit{km}$，仰角是 $30°$． $n$秒后，火箭到达 $B$点，此时仰角是 $45°$，则火箭在这 $n$秒中上升的高度是　　 $\mathit{km}$．

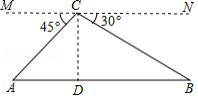
如图，某校教学楼 AC与实验楼 BD的水平间距 CD＝15 $\sqrt{3}$ 米，在实验楼顶部 B点测得教学楼顶部 A点的仰角是30°，底部 C点的俯角是45°，则教学楼 AC的高度是 　米（结果保留根号）．

全球最大的关公塑像矗立在荆州古城东门外．如图，张三同学在东门城墙上C处测得塑像底部B处的俯角为11°48′，测得塑像顶部A处的仰角为45°，点D在观测点C正下方城墙底的地面上，若CD＝10米，则此塑像的高AB约为　　米（参考数据：tan78°12′≈4.8）．

如图，航拍无人机从 $A$ 处测得一幢建筑物顶部 $C$ 的仰角是 $30°$ ，测得底部 $B$ 的俯角是 $60°$ ，此时无人机与该建筑物的水平距离 $\mathit{AD}$ 是9米，那么该建筑物的高度 $\mathit{BC}$ 为 　　米（结果保留根号）．

如图，航拍无人机从 $A$ 处测得一幢建筑物顶部 $C$ 的仰角是 $30°$ ，测得底部 $B$ 的俯角是 $60°$ ，此时无人机与该建筑物的水平距离 $\mathit{AD}$ 是9米，那么该建筑物的高度 $\mathit{BC}$ 为 　　米（结果保留根号）．

如图，测角仪竖直放在距建筑物底部的位置，在处测得建筑物顶端的仰角为．若测角仪的高度是，则建筑物的高度约为　　．（结果保留小数点后一位，参考数据：，，

如图，在处利用测角仪测得某建筑物的顶端点的仰角为，点的仰角为，点到建筑物的距离为米，则　　米．

如图，为测量旗杆的高度，在教学楼一楼点处测得旗杆顶部的仰角为，在四楼点处测得旗杆顶部的仰角为，点与点在同一水平线上．已知，则旗杆的高度为　　．

）如图，小明为了测量校园里旗杆的高度，将测角仪竖直放在距旗杆底部点的位置，在处测得旗杆顶端的仰角为，若测角仪的高度是，则旗杆的高度约为　　．（精确到．参考数据：，，

如图，在量角器的圆心处下挂一铅锤，制作了一个简易测倾仪．量角器的0刻度线对准楼顶时，铅垂线对应的读数是，则此时观察楼顶的仰角度数是　　．