初中数学解直角三角形解答题

（1）计算：3sin30°－2cos45°+tan²60⁰;
（2）在Rt△ABC中，∠C＝90° , c＝20，∠A=30° , 解这个直角三角形.

计算或化简求值
（1）
（2）先化简：,其中

（本小题满分8分）如图，湖中有一小岛，湖边有一条笔直的观光小道AB，现决定从小岛架一座与观光小道垂直的小桥PD，在小道上测得如下数据：AB=60米，∠PAB=45°，∠PBA=30°．请求出小桥PD的长．

如图，在矩形ABCD中，AC,BD交于点O，若BO=3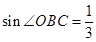，，求矩形ABCD的面积.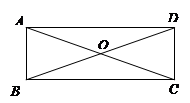

如图，在教学实践课中，小明为了测量学校旗杆CD的高度，在地面A处放置高度为1.5米的测角仪AB，测得旗杆顶端D的仰角为32°，AC=22米，求旗杆CD的高度．（结果精确到0.1米．参考数据：sin32°≈0.53，cos32°≈0.85，tan32°≈0.62）

如图所示，在A岛周围25海里的范围内有暗礁．一轮船由西向东航行到B处时，发现A岛在北偏东60°方向，轮船继续前行20海里，到达C处，发现A岛在北偏东45°方向，该船若不改变航向继续前行，有无触礁的危险？（结果精确到0.1海里）

请阅读下列材料：
问题：如图（1），圆柱的底面半径为4cm，圆柱高AB为2cm，BC是底面直径，求一只蚂蚁从点A出发沿圆柱表面爬行到点C的最短路线，小明设计了两条路线：
路线1：高线AB+底面直径BC，如图（1）所示．
路线2：侧面展开图中的线段AC，如图（2）所示．

设路线1的长度为l₁，则l₁=AB+BC=2+8=10；
设路线2的长度为l₂，则l₂===；
∵=10²﹣（4+16π²）=96﹣16π²=16（6﹣π²）＜0
∴即l₁＜l₂
所以选择路线1较短．
（1）小明对上述结论有些疑惑，于是他把条件改成：“圆柱的底面半径为2cm，高AB为4cm”继续按前面的路线进行计算．（结果保留π）
①此时，路线1：l₁=        ．路线2：l₂=             ．
②所以选择哪条路线较短？试说明理由．
（2）请你帮小明继续研究：当圆柱的底面半径为2cm，高为hcm时，应如何选择上面的两条路线才能使蚂蚁从点A出发沿圆柱表面爬行到点C的路线最短．

（1）已知，求的值.
（2）已知是锐角△ABC的三个内角，且满足，求的度数.

（本题7分）先化简，再求值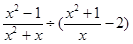：，其中x=2cos30°+tan45.

为解决江北学校学生上学过河难的问题，乡政府决定修建一座桥，建桥过程中需测量河的宽度（即两平行河岸AB与MN之间的距离）．在测量时，选定河对岸MN上的点C处为桥的一端，在河岸点A处，测得∠CAB=30°，沿河岸AB前行30米后到达B处，在B处测得∠CBA=60°，请你根据以上测量数据求出河的宽度．（参考数据：≈1.41，≈1.73，结果保留整数）

（1）计算：+ sin45°·cos45°     
（2）解方程：x²−5x −6 = 0

（1）计算：2014﹣（﹣1）²⁰¹⁴+﹣|﹣3|
（2）先化简，再求值：﹣÷，其中x=4cos60°+1．

（本小题满分6分）如图，有两棵树，一棵高10米，另一棵高4米，两树相距8米，一只小鸟从一棵树的树梢飞到另一棵树的树梢，求小鸟至少飞行的距离．
 

（本题共有2小题，每小题4分，共8分）
（1）计算：；    
（2）解方程组： 

（1）计算：
（2）先化简，再求值：