[江苏]2014届江苏省江阴市顾山九年级上学期期末考试数学试卷
已知x=1是一元二次方程x2-2mx+1=0的解,则m的值是
| A.-1 | B.0 | C.1 | D.0或1 |
下列命题中,正确命题的序号是
①一组对边平行且相等的四边形是平行四边形
②一组邻边相等的平行四边形是正方形
③对角线互相垂直且相等的四边形是菱形
④任何三角形都有外接圆,但不是所有的四边形都有外接圆
| A.①② | B.②③ | C.③④ | D.①④ |
甲、乙、丙、丁四名射击运动员参加射击预选赛,他们射击成绩的平均环数 及方差
及方差 如下表所示.
如下表所示.
| |
甲 |
乙 |
丙 |
丁 |
 |
8 |
9 |
9 |
8 |
 |
1 |
1 |
1.2 |
1.3 |
若要选出一个成绩较好且状态稳定的运动员去参赛,那么应选运动员
A.甲 B.乙 C.丙 D.丁
已知两圆的半径是方程x2-7x+12=0的两根,圆心距为8,那么这两个圆的位置关系是
| A.内切 | B.外离 | C.相交 | D.外切 |
已知二次函数 的图象与x轴没有交点,则k的取值范围为
的图象与x轴没有交点,则k的取值范围为
A.k﹥- |
B.k≥- 且k≠0 且k≠0 |
C.k﹤- |
D.k﹥- 且k≠0 且k≠0 |
有下列四个命题:① 直径是弦;② 经过三个点一定可以作圆;③ 三角形的外心到三角形各边的距离相等;④平分弦的直径垂直于弦.其中正确的有
| A.4个 | B.3个 | C.2个 | D.1个 |
如图所示,直线CD与线段AB为直径的圆相切于点D,并交BA的延长线于点C,且AB=2,AD=1,P点在切线CD上移动.当∠APB的度数最大时,则∠ABP的度数为
| A.90° | B.60° | C.45° | D.30° |
.如图,在10×10的网格中,每个小方格都是边长为1的小正方形,每个小正方形的顶点称为格点.若抛物线经过图中的三个格点,则以这三个格点为顶点的三角形称为抛物线的“内接格点三角形”.以O为坐标原点建立如图所示的平面直角坐标系,若抛物线与网格对角线OB的两个交点之间的距离为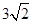 ,且这两个交点与抛物线的顶点是抛物线的内接格点三角形的三个顶点,则满足上述条件且对称轴平行于y轴的抛物线条数是
,且这两个交点与抛物线的顶点是抛物线的内接格点三角形的三个顶点,则满足上述条件且对称轴平行于y轴的抛物线条数是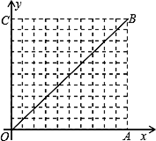
| A.13 | B.14 | C.15 | D.16 |
如图,一种电子游戏,电子屏幕上有一正方形ABCD,点P沿直线AB左右移动,当出现:点P与正方形四个顶点中的任意两个顶点构成等腰三角形时,就会发出警报,则直线AB上会发出警报的点P有 个. 
如图,矩形ABCD中,点E,F,G,H分别在边AB,BC,CD,DA上,点P在矩形ABCD内.若AB=4cm,BC=6cm,AE=CG=3cm,BF=DH=4cm,四边形AEPH的面积为8cm2,则四边形PFCG的面积为________cm2.
如图,在平行四边形ABCD中,点E,F分别是AB,CD的中点.
(1)求证:四边形AEFD是平行四边形;(2)若∠A=60°,AB=2AD=4,求BD的长.
如图,在单位长度为1的正方形网格中建立一直角坐标系,一条圆弧经过网格点A、B、C,请在网格图中进行下列操作(以下结果保留根号):
(1)利用网格确定该圆弧所在圆的圆心D点的位置,并写出D点的坐标为 ;
(2)连接AD、CD,则⊙D的半径为 ,∠ADC的度数为 ;
(3)若扇形DAC是一个圆锥的侧面展开图,求该圆锥底面半径.
2013年12月13日凌晨1点26分,某地煤矿发生瓦斯爆炸事故,该地救援队立即赶赴现场进行救援,救援队利用生命探测仪在地面A、B两个探测点探测到C处有生命迹象.已知A、B两点相距4米,探测线与地面的夹角分别是30°和45°,试确定生命所在点C的深度.(精确到0.1米)
某商场经营某种品牌的玩具,购进时的单价是30元,根据市场调查:在一段时间内,销售单价是40元时,销售量是600件,而销售单价每涨1元,就会少售出10件玩具.
(1)不妨设该种品牌玩具的销售单价为x元(x > 40),请你分别用x的代数式来表示销售量y件和销售该品牌玩具获得利润w元,并把结果填写在表格中:
| 销售单价(元) |
x |
| 销售量y(件) |
|
| 销售玩具获得利润w(元) |
|
(2)在(1)条件下,若商场获得了10000元销售利润,求该玩具销售单价x应定为多少元?
(3)在(1)条件下,若玩具厂规定该品牌玩具销售单价不低于44元,且商场要完成不少于540件的销售任务,求商场销售该品牌玩具获得的最大利润是多少?
如图,在△ABC中,AB=AC,以AB为直径作半圆⊙0,交BC于点D,连接AD,过点D作DE⊥AC,垂足为点E,交AB的延长线于点F.
(1)求证:EF是⊙0的切线.(2)如果⊙0的半径为5,sin∠ADE= ,求BF的长.
,求BF的长.
已知抛物线y=ax2+bx+c(a≠0)的顶点坐标为(4,﹣ ),且与y轴交于点C(0,2),与x轴交于A,B两点(点A在点B的左边).
),且与y轴交于点C(0,2),与x轴交于A,B两点(点A在点B的左边).
(1)求抛物线的解析式及A,B两点的坐标;
(2)在(1)中抛物线的对称轴l上是否存在一点P,使AP+CP的值最小?若存在,求AP+CP的最小值,若不存在,请说明理由;
阅读下面材料:
小明遇到这样一个问题:如图1,在边长为 的正方形ABCD各边上分别截取AE=BF=CG=DH=1,当∠AFQ=∠BGM=∠CHN=∠DEP=45°时,求正方形MNPQ的面积.小明发现:分别延长QE,MF,NG,PH,交FA,GB,HC,ED的延长线于点R,S,T,W,可得△RQF,△SMG,△TNH,△WPE是四个全等的等腰直角三角形(如图2)
的正方形ABCD各边上分别截取AE=BF=CG=DH=1,当∠AFQ=∠BGM=∠CHN=∠DEP=45°时,求正方形MNPQ的面积.小明发现:分别延长QE,MF,NG,PH,交FA,GB,HC,ED的延长线于点R,S,T,W,可得△RQF,△SMG,△TNH,△WPE是四个全等的等腰直角三角形(如图2)

请回答:
(1)若将上述四个等腰直角三角形拼成一个新的正方形(无缝隙,不重叠),则这个新的正方形的边长为__________;
(2)求正方形MNPQ的面积.
参考小明思考问题的方法,解决问题:
如图3,在等边△ABC各边上分别截取AD=BE=CF,再分别过点D,E,F作BC,AC,AB的垂线,得到等边△RPQ,若 ,则AD的长为__________.
,则AD的长为__________.
如图,在平面直角坐标系中,矩形OABC的两边OA、OC分别在x轴、y轴的正半轴上,OA=4,OC=2.点P从点O出发,沿x轴以每秒1个单位长的速度向点A匀速运动,当点P到达点A时停止运动,设点P运动的时间是t秒.将线段CP的中点绕点P按顺时针方向旋转90°得点D,点D随点P的运动而运动,连接DP、DA.
(1)请用含t的代数式表示出点D的坐标;
(2)求t为何值时,△DPA的面积最大,最大为多少?
(3)在点P从O向A运动的过程中,△DPA能否成为直角三角形?若能,求t的值.
若不能,请说明理由;
(4)请直接写出随着点P的运动,点D运动路线的长.




 ,则cos∠A的值为
,则cos∠A的值为



 有意义的
有意义的 的取值范围为 .
的取值范围为 . 有实数根,则
有实数根,则 的取值范围为 .
的取值范围为 . ,点A为弦BC所对劣弧上任意一点. 则∠BAC的度数为 .
,点A为弦BC所对劣弧上任意一点. 则∠BAC的度数为 .  中,
中, 为
为 的内切圆,点
的内切圆,点 斜边
斜边 的中点,则
的中点,则 .
. 

 ,其中
,其中
 粤公网安备 44130202000953号
粤公网安备 44130202000953号