江苏省兴化顾庄等三校九年级上学期期末考试数学试卷

一名射击爱好者5次射击的中靶环数如下：6，7，9，8，9，这5个数据的中位数是（ ）. 

掷一个骰子时，点数小于2的概率是（ ）.

A．

B．

C．

D．0

下列说法中，正确的是（    ）.

如图，坡角为的斜坡上两树间的水平距离AC为，则两树间的坡面距离AB为（ ）.

A．

B．

C．

D．

若两个相似多边形的面积之比为1：4，则它们的周长之比为（ ）.

如图，在平面直角坐标系中，抛物线y=经过平移得到抛物线y=，其对称轴与两段抛物线所围成的阴影部分的面积为（ ）.

在比例尺为1：10000000的地图上，量得甲、乙两地的距离是30厘米，则两地的实际距离
是   千米.

已知x ：y ="2" ：3，则(x+y) ：y 的值为   .

一个不透明的袋中装有2枚白色棋子和n枚黑色棋子，它们除颜色不同外，其余均相同．若小明从中随机摸出一枚棋子，多次实验后发现摸到黑色棋子的频率稳定在80%．则n很可能是   枚．

在△ABC中，∠C=90°，BC=2，，则边AC的长是   ．

某居民小区为了了解本小区100户居民家庭平均月使用塑料袋的数量情况，随机调査了10户居民家庭月使用塑料袋的数量，结果如下：（単位：只）
65    70   85   74   86   78   74   92   82    94
根据统计情况，估计该小区这100户家庭平均使用塑料袋      只． 

在某一时刻，测得一根高为1.8m的竹竿的影长为3m，同时测得一根旗杆的影长为25m，那么这根旗杆的高度为   m．  

如图，抛物线的对称轴是直线，与x轴交于A、B两点，若B点坐标是，则A点的坐标是   .
 

如图，PA、PB分别与⊙O相切于点A、B，⊙O的切线EF分别交PA、PB于点E、F，切点C在上，若PA长为2，则△PEF的周长是   ．

若粮仓顶部是圆锥形，且这个圆锥的高为2m，母线长为2.5m，为防雨需在粮仓顶部铺上油毡，则这块油毡的面积是    m². 

如图，Rt△ABC中，∠ACB=90°，∠ABC=60°，BC=2cm，D为BC的中点，若动点E以1cm/s的速度从A点出发，沿着A→B→A的方向运动，设E点的运动时间为t秒（0≤t＜6），连接DE，当△BDE是直角三角形时，t的值为（ ）

（1）计算：3sin30°－2cos45°+tan²60⁰;
（2）在Rt△ABC中，∠C＝90° , c＝20，∠A=30° , 解这个直角三角形.

甲、乙两人在相同的条件下各射靶10次，每次命中的环数如下：
甲：9，7，8，9，7，6，10，10，6，8； 乙：7，8，8，9，7，8，9，8，10，6
（1）分别计算甲、乙两组数据的方差；
（2）根据计算结果比较两人的射击水平．

在一个不透明的布口袋中装有只有颜色不同，其他都相同的白、红、黑三种颜色的小球各只，甲、乙两人进行摸球游戏:甲先从袋中摸出一球,看清颜色后放回，再由乙从袋中摸出一球．
（1）试用树状图（或列表法）表示摸球游戏所有可能的结果；
（2）如果规定：乙摸到与甲相同颜色的球为乙胜，否则为甲胜，问谁在游戏中获胜的可能性更大些？

某课题组为了解全市九年级学生对数学知识的掌握情况,在一次数学检测中,从全市20000名九年级考生中随机抽取部分考生的数学成绩进行调查,并将调查结果绘制成如下图表:

分数段	频数	频率
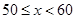	20	0.10
	28	b
	54	0.27
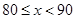	a	0.20
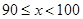	24	0.12
	18	0.09
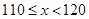	16	0.08

(1)表中a和b所表示的数分别为a=         ,b=         ;
(2)请在图中补全频数分布直方图;
(3)如果把成绩在70分以上(含70分)定为合格,那么该市20000名九年级考生数学成绩为合格的考生约有多少名?

如图，某居民小区有一朝向为正南方向的居民楼，该居民楼的一楼是高米的小区超市，超市以上是居民住房，在该楼的前面米处要盖一栋高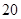米的新楼．当冬季正午的阳光与水平线的夹角为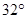时．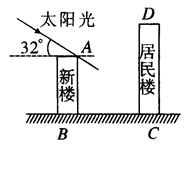

（）问超市以上的居民住房采光是否有影响，为什么？
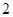（）若要使超市采光不受影响，两楼应相距多少米？
（参考数据：sin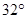≈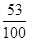，cos≈≈．）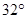

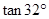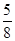(10分) 如图，已知二次函数y=ax²+bx+c的图像过A（2，0），B（0，﹣1）和C（4，5）三点．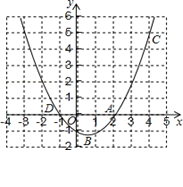

（1）求二次函数的解析式；
（2）设二次函数的图像与x轴的另一个交点为D，求点D的坐标；
（3）在同一坐标系中画出直线y=x+1，并写出当x在什么范围内时，一次函数的值大于二次函数的值．

一块直角三角形木版的一条直角边AB为3m，面积为6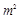，要把它加工成一个面积最大的正方形桌面，小明打算按图①进行加工，小华准备按图②进行裁料，他们谁的加工方案符合要求?
 
图①                      图②

）如图，在△ABC中，AB=AC，以AB为直径作半圆⊙0，交BC于点D，连接AD，过点D作DE⊥AC，垂足为点E，交AB的延长线于点F．

（1）求证：EF是⊙0的切线;
（2）如果⊙0的半径为9，sin∠ADE=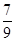，求AE的长．

如图所示，E是正方形ABCD的边AB上的动点，正方形的边长为4， EF⊥DE交BC于点F．
   
（1）求证：△ADE ∽△BEF ；
（2）AE=x，BF=y．当x取什么值时，y有最大值? 并求出这个最大值;
（3）已知D、C 、F、E四点在同一个圆上，连接CE、DF，若sin∠CEF =，求此圆直径．

如图，抛物线y=ax²+bx+c经过点A(﹣3，0)，B(1.0)，C(0，﹣3)．

(1)求抛物线的解析式；
(2)若点P为第三象限内抛物线上的一点，设△PAC的面积为S，求S的最大值并求出此时点P的坐标；
(3)设抛物线的顶点为D，DE⊥x轴于点E，在y轴上是否存在点M，使得△ADM是直角三角形？若存在，请直接写出点M的坐标；若不存在，请说明理由．