如图,某居民小区有一朝向为正南方向的居民楼,该居民楼的一楼是高 米的小区超市,超市以上是居民住房,在该楼的前面
米的小区超市,超市以上是居民住房,在该楼的前面 米处要盖一栋高
米处要盖一栋高 米的新楼.当冬季正午的阳光与水平线的夹角为
米的新楼.当冬季正午的阳光与水平线的夹角为 时.
时.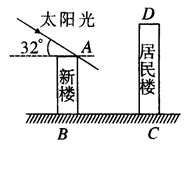
(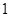 )问超市以上的居民住房采光是否有影响,为什么?
)问超市以上的居民住房采光是否有影响,为什么?
( )若要使超市采光不受影响,两楼应相距多少米?
)若要使超市采光不受影响,两楼应相距多少米?
(参考数据:sin ≈
≈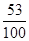 ,cos
,cos ≈
≈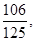
 ≈
≈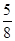 .)
.)
相关知识点
推荐套卷
如图,某居民小区有一朝向为正南方向的居民楼,该居民楼的一楼是高 米的小区超市,超市以上是居民住房,在该楼的前面
米的小区超市,超市以上是居民住房,在该楼的前面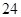 米处要盖一栋高
米处要盖一栋高 米的新楼.当冬季正午的阳光与水平线的夹角为
米的新楼.当冬季正午的阳光与水平线的夹角为 时.
时.
(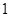 )问超市以上的居民住房采光是否有影响,为什么?
)问超市以上的居民住房采光是否有影响,为什么?
( )若要使超市采光不受影响,两楼应相距多少米?
)若要使超市采光不受影响,两楼应相距多少米?
(参考数据:sin ≈
≈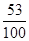 ,cos
,cos ≈
≈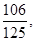
 ≈
≈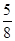 .)
.)