初中数学解直角三角形解答题

（请在下列两个小题中,任选其一完成即可）
(1)求不等式组的整数解．
(2)计算：

（1）计算： $(-1{)}^{2015}-\sqrt{9}+(3-\pi {)}^0+|3-\sqrt{3}|+(\tan 30°{)}^{-1}$
（2）解方程组： $\left\{\begin{array}{l}x+y=6\\ 2x-y=9\end{array}\right.$

计算：（1）(－3)²－＋(－1)⁰+
（2）

（每小题4分，共8分）
（1）计算：
（2）化简  

⑴计算：   ⑵化简：

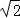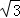如图，某塔观光层的最外沿点E为蹦极项目的起跳点．已知点E离塔的中轴线AB的距离OE为10米，塔高AB为123米（AB垂直地面BC），在地面C处测得点E的仰角α=45°，从点C沿CB方向前行40米到达D点，在D处测得塔尖A的仰角β=60°，求点E离地面的高度EF．（结果精确到1米，参考数据≈1．4，≈1．7）

（1）计算：tan45º－(－2)²－；
（2）已知x²－4x－1=0，求代数式(2x－3)²－(x＋y)(x－y)－y²的值

（1）计算：（）⁰ - （）^-2 + ；
（2）解方程： - = 2．

（本小题满分10分。每题5分）
（1）计算：；
（2）解方程：

为解决江北学校学生上学过河难的问题，乡政府决定修建一座桥，建桥过程中需测量河的宽度（即两平行河岸AB与MN之间的距离）．在测量时，选定河对岸MN上的点C处为桥的一端，在河岸点A处，测得∠CAB=30°，沿河岸AB前行30米后到达B处，在B处测得∠CBA=60°，请你根据以上测量数据求出河的宽度．（参考数据：≈1.41，≈1.73，结果保留整数）

（1）计算：+ sin45°·cos45°     
（2）解方程：x²−5x −6 = 0

（1）计算：2014﹣（﹣1）²⁰¹⁴+﹣|﹣3|
（2）先化简，再求值：﹣÷，其中x=4cos60°+1．

（本小题满分6分）如图，有两棵树，一棵高10米，另一棵高4米，两树相距8米，一只小鸟从一棵树的树梢飞到另一棵树的树梢，求小鸟至少飞行的距离．
 

（本题共有2小题，每小题4分，共8分）
（1）计算：；    
（2）解方程组： 

（1）计算：
（2）先化简，再求值：