初中数学解直角三角形解答题

计算：

计算：
（1）
（2）

丁丁要制作一个形如图1所示的风筝，想在一个矩形材料中裁剪出如图2阴影所示的梯形翅膀，请你根据图2中的数据帮丁丁计算出BE、CD的长度（精确到个位，≈1.7）

(1)计算：++(－1)⁰-2sin45°  
(2)先化简，再求值： ，其中

如图，梯形ABCD中，AD∥BC，，BC=2，，．

(1) 求∠BDC的度数；  (2) 求AB的长．

据交管部门统计，高速公路超速行驶是引发交通事故的主要原因．我市某校数学课外小组的几个同学想尝试用自己所学的知识检测车速，甬台温高速公路温州—瑞安路段的限速是：每小时80千米（即最高时速不超过80千米），如图，他们将观测点设在离公路L的距离为0.1千米的P处．这时，一辆轿车由温州向瑞安匀速直线驶来，测得此车从A处行驶到B处所用的时间为3秒，并测得∠APO＝60°，∠BPO＝45°．试计算AB的长度并判断此车是否超速？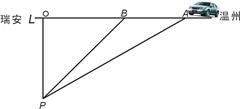

2010年4月14日上午7时49分，青海省藏族自治州玉树县发生里氏7.1级地震。某省地震救援队立即赶赴震区进行救援。救援队利用生命探测仪在某建筑物废墟下方探测出点 C 处有生命迹象，已知废墟一侧地面上两探测点A、B 相距3米，探测线与地面的夹角分别是30°和 60°（如图），试确定生命所在点 C 的深度．
（结果精确到0.1米，参考数据：）  
 

校车安全是近几年社会关注的重大问题，安全隐患主要是超速和超载．九台三十一中学九年一班数学活动小组设计了如下检测公路上行驶的汽车速度的实验：先在公路旁边选取一点C，再在笔直的车道上确定点D，使CD与垂直，测得CD长等于18米，在上点D的同侧取点A、B，使∠CAD=30°，∠CBD=60°．

(1) 求AB的长（精确到0.1米，参考数据=1.73，=1.41）；
(2)已知本路段对校车限速为40千米/小时，若测得某辆校车从A到B用时2秒，这辆校车是否超速？说明理由．

如图，，矩形ABCD的顶点A、B分别在边OM 、ON上运动，且形状和大小保持不变，其中AB=4，BC=3.

（1）当时，OA的长为         ；
（2）连接AC，当∥时，求OA的长；
（3）设AB边的中点为E，分别求出OA、OB、OC、OD、OE在运动过程中的长度变化范围.

如图，在某校办公楼AC前，挂着“海西先行多做贡献——教育为先；南安创新争当榜样——育人为本”的宣传条幅AB,在距楼底C处15米的地面上一点D,测得条幅顶端A的仰角为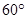,条幅底端B的仰角为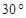，求宣传条幅AB的长度.（计算结果精确到0.1米）．

如图，自来水公司的主管道从A小区向北偏东60°方向直线延伸，测绘员在A处测得要安装自来水的M小区在A小区北偏东30°方向，测绘员沿主管道步行8000米到达C处，测得小区M位于C的北偏西60°方向，请你（不写作法，保留作图痕迹）找出支管道连接点N，使到该小区铺设的管道最短，并求出AN的长．

如图，为测楼房BE的高，用测量仪在距楼底部30米的D处，用高1.2米的测角仪测得楼顶B的仰角α为60°.求楼房BE的高度.（精确到0.1米）.

在一次课外实践活动中，同学们要测量某公园人工湖两侧A，B两个凉亭之间的距离．现测得AC=30m，BC=70m，∠CAB=120°，请计算A，B两个凉亭之间的距离．

（1）计算：2sin60°－＋()^－1＋(－1)²⁰⁰⁸
（2）解方程：

已知，，，，请从，，，这4个数中任意选取3个求积，有多少种不同的结果？