[江苏]2013届江苏省南京学大教育专修学校九年级3月月考数学试卷
如图,△ABC中,P是AB边上的一点,连结CP.添加一个条件使△ACP与△ABC相似.下列添加的条件中不正确的是( )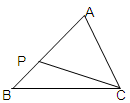
| A.∠APC=∠ACB | B.∠ACP=∠B | C.AC2=AP·AB | D.AC:PC=AB:BC |
如图,抛物线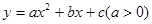 的对称轴是直线
的对称轴是直线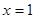 ,且经过点
,且经过点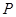 (3,0),则
(3,0),则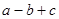 的值为( )
的值为( )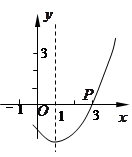
| A.0 | B.-1 | C. 1 | D. 2 |
如图,正三角形ABC内接于⊙O,动点P在圆周的劣弧AB上,且不与A、B重合,则∠BPC等于( )
A.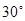 B.
B.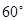 C.
C.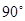 D.
D.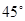
如图,二次函数  的图像与
的图像与 轴有一个交点在0和1之间(不含0
轴有一个交点在0和1之间(不含0
和1),则 的取值范围是( )
的取值范围是( )
A. |
B. |
C. |
D. |
在正方形ABCD中,点E为BC边的中点,点 与点B关于AE对称,
与点B关于AE对称, 与AE交于点F,连接
与AE交于点F,连接 ,
, ,FC。下列结论:①
,FC。下列结论:① ;②
;② 为等腰直角三角形;③
为等腰直角三角形;③ ;④
;④ 。其中正确的是( )
。其中正确的是( )
| A.①② | B.①②④ | C.③④ | D.①②③④ |
小明有黑色、白色、蓝色西服各一件,有红色、黄色领带各一条,从中分别取一件西服和一条领带,则小明穿黑色西服打红色领带的概率是 .
如图,△ 为⊙O的内接三角形,AB为⊙O的直径,点D在⊙O 上,∠BAC=35°,则∠ADC= 度.
为⊙O的内接三角形,AB为⊙O的直径,点D在⊙O 上,∠BAC=35°,则∠ADC= 度.
如图,AB是⊙O的直径,点C在AB的延长线上,CD与⊙O相切于点D.若∠C=18°,则∠CDA=_________度.
如图,将半径为2、圆心角为 的扇形纸片
的扇形纸片 ,在直线
,在直线 上向右作无滑动的滚动至扇形
上向右作无滑动的滚动至扇形 处,则顶点
处,则顶点 经过的路线总长为 。
经过的路线总长为 。
现有两个纸箱,每个纸箱内各装有4个材质、大小都相同的乒乓球,其中一个纸箱内4个小球上分别写有1、2、3、4这4个数,另一个纸箱内4个小球上分别写有5、6、7、8这4个数,甲、乙两人商定了一个游戏,规则是:从这两个纸箱中各随机摸出一个小球,然后把两个小球上的数字相乘,若得到的积是2的倍数,则甲得1分,若得到积是3的倍数,则乙得2分.完成一次游戏后,将球分别放回各自的纸箱,摇匀后进行下一次游戏,最后得分高者胜出.。
(1)请你通过列表(或树状图)分别计算乘积是2的倍数和3的倍数的概率;
(2)你认为这个游戏公平吗?为什么?若你认为不公平,请你修改得分规则,使游戏对双方公平.
如图矩形ABCD中,过A,B两点的⊙O切CD于E,交BC于F,AH⊥BE于H,连结EF。
⑴ 求证:∠CEF=∠BAH,⑵若BC=2CE=6,求BF的长。
如图,已知在⊙O中,AB=4 ,AC是⊙O的直径,AC⊥BD于F,∠A=30°
,AC是⊙O的直径,AC⊥BD于F,∠A=30°
(1)求图中阴影部分的面积;
(2)若用阴影扇形OBD围成一个圆锥侧面,请求出这个圆锥的底面圆的半径。
如图,已知AB是⊙O的直径,点C在⊙O上,P是△OAC的重心,且OP= ,∠A=30º.
,∠A=30º.

(1)求劣弧 的长;
的长;
(2)若∠ABD=120º,BD=1,求证:CD是⊙O的切线.
某果品基地用汽车装运A、B、C三种不同品牌的水果到外地销售,按规定每辆汽车只能装同种水果,且必须装满,其中A、B、C三种水果的重量及利润按下表提供信息:
| 水果品牌 |
A |
B |
C |
| 每辆汽车载重量(吨) |
2.2 |
2.1 |
2 |
| 每吨水果可获利润(百元) |
6 |
8 |
5 |
(1)若用7辆汽车装运A、C两种水果共15吨到甲地销售,如何安排汽车装运A、C两种水果?
(2)计划用20辆汽车装运A、B、C三种不同水果共42吨到乙地销售(每种水果不少于2车),请你设计一种装运方案,可使果品基地获得最大利润,并求出最大利润。
已知抛物线y=ax2+bx+c与x轴交于A、B两点,与y轴交于点C,其中点B在x轴的正半轴上,点C在y轴的正半轴上,线段OB、OC的长(OB<OC)是方程x2-10x+16=0的两个根,且抛物线的对称轴是直线x=-2.
(1)求A、B、C三点的坐标;
(2)求此抛物线的表达式;
(3)连接AC、BC,若点E是线段AB上的一个动点(与点A、点B不重合),过点E作EF∥AC交BC于点F,连接CE,设AE的长为m,△CEF的面积为S,求S与m之间的函数关系式,并写出自变量m的取值范围;
(4)在(3)的基础上试说明S是否存在最大值,若存在,请求出S的最大值,并求出此时点E的坐标,判断此时△BCE的形状;若不存在,请说明理由.
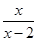 有意义,则x的取值范围是( )
有意义,则x的取值范围是( )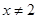
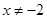
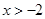
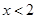
 的解为 .
的解为 . 的图象经过点(-2,5),则k=________.
的图象经过点(-2,5),则k=________.
 +(
+( )-1+(-1)2008
)-1+(-1)2008
 的半径为1,以
的半径为1,以 ,顶点
,顶点 的坐标为(
的坐标为( ,0),顶点
,0),顶点 在
在 轴上方,顶点
轴上方,顶点 在⊙
在⊙
 与⊙
与⊙ 所在直线对应的函数表达式;如果不相切,也请说明理由;
所在直线对应的函数表达式;如果不相切,也请说明理由; ,求出
,求出 粤公网安备 44130202000953号
粤公网安备 44130202000953号