如图1,在矩形 中,点 在 上, ,点 从点 出发,沿 的路径匀速运动到点 停止,作 于点 ,设点 运动的路程为 , 长为 ,若 与 之间的函数关系图象如图2所示,当 时, 的值是

A.2B. C. D.1
如图,由四个全等的直角三角形围成的大正方形的面积是169,小正方形的面积为49,则
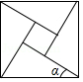
A. B. C. D.
如图, 、 、 是小正方形的顶点,且每个小正方形的边长为1,则 的值为

A. B.1C. D.
如图,矩形 绕点 逆时针旋转 后得到矩形 , 与 交于点 ,延长 交 于 ,若 , ,则 的长度为

A. B. C. D.
如图, 是 的直径,弦 于点 , , 的半径为 ,则圆心 到弦 的距离为

A. B. C. D.
如图,在菱形 中,对角线 与 相交于点 ,若 , ,则 的长为

A.2B.3C. D.
如图,在 中, 是 边上的点,以 为圆心, 为半径的 与 相切于点 , 平分 , , , 的长是

A. B.2C. D.
如图,在 中, ,将 绕顶点 逆时针旋转得到△ , 是 的中点, 是 的中点,连接 .若 , ,则线段 的最大值是
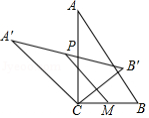
A.4B.3C.2D.1
如图, 过点 , , , ,点 是 轴下方 上的一点,连接 , ,则 的度数是
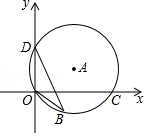
A. B. C. D.
一组正方形按如图所示的方式放置,其中顶点 在 轴上,顶点 、 、 、 、 、 、 在 轴上,已知正方形 的边长为1, , 则正方形 的边长是

A. B. C. D.
如图,沿 方向开山修建一条公路,为了加快施工进度,要在小山的另一边寻找点 同时施工,从 上的一点 取 ,沿 的方向前进,取 ,测得 , ,并且 , 和 在同一平面内,那么公路 段的长度为

A. B. C. D.
小明利用测角仪和旗杆的拉绳测量学校旗杆的高度.如图,旗杆PA的高度与拉绳PB的长度相等.小明将PB拉到PB′的位置,测得 (B′C为水平线),测角仪B′D的高度为1米,则旗杆PA的高度为( )

A. B. C. D.