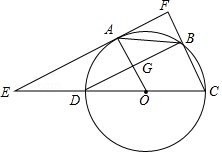
如图,已知 的直径 , , 为圆周上两点,且四边形 是平行四边形,过 点作直线 ,分别交 , 的延长线于点 , , 与 交于 点.
(1)求证: 是 的切线;
(2)求 的长.
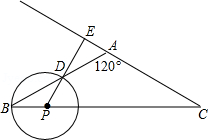
如图, 中, , . 是底边 上的一个动点 与 、 不重合),以 为圆心, 为半径的 与射线 交于点 ,射线 交射线 于点 .
(1)若点 在线段 的延长线上,设 , ,求 关于 的函数关系式,并写出 的取值范围.
(2)当 时,试说明射线 与 是否相切.
(3)连接 ,若 ,求 的长.
如图,矩形 绕点 逆时针旋转 后得到矩形 , 与 交于点 ,延长 交 于 ,若 , ,则 的长度为

A. B. C. D.
如图, 是 的直径,弦 于点 , , 的半径为 ,则圆心 到弦 的距离为

A. B. C. D.
如图,在菱形 中,对角线 与 相交于点 ,若 , ,则 的长为

A.2B.3C. D.
如图,在 中, 为直径, 、 为圆上两点, 为圆外一点,且 .
(1)求证: 为 的切线.
(2)若 , ,求 的半径.

(2) , ,
,
;
又 ,
,
;
方法一:在 中, ,
连接 ,设 的半径为 ,则在 中, ,即
解得:
方法二: ,过点 作 于点 ,则
在 中,

本题考查了圆的综合题:圆的切线垂直于过切点的半径;利用勾股定理计算线段的长.
如图,在 中,以 为直径作 交 于点 , .
(1)求证: 是 的切线;
(2)点 是 上一点,若 , , 的半径是4,求 的长.
