如图,在矩形纸片中,
,
,点
在
上,将
沿
折叠,点
恰落在边
上的点
处;点
在
上,将
沿
折叠,点
恰落在线段
上的点
处,有下列结论:
①;②
;③
;④
.
其中正确的是 .(把所有正确结论的序号都选上)

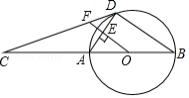
如图,为
的直径,
为
延长线上一点,
是
的切线,
为切点,
于点
,交
于点
.
(1)求证:;
(2)若,
,求
的长.
如图,在平行四边形ABCD中,点E在AD上,连接CE并延长与BA的延长线交于点F,若AE=2ED,CD=3cm,则AF的长为( )

| A.5cm | B.6cm | C.7cm | D.8cm |
如图,在x轴的上方,直角∠BOA绕原点O按顺时针方向旋转,若∠BOA的两边分别与函数y=﹣ 、y=
、y= 的图象交于B、A两点,则∠OAB的大小的变化趋势为( )
的图象交于B、A两点,则∠OAB的大小的变化趋势为( )

A.逐渐变小 B.逐渐变大 C.无法确定 D.保持不变
如图1,△ABC中,BC=25,BC边上的高为20,将AB,AC分别n等分,连接两边对应的等分点,以这些连接线为一边做矩形,使这些矩形的边B1C1,B2C2,B3C3……的对应边分别为 B2C2,B3C3,B4C4……
(1)若n=5,如图2,求B3C3为一边的矩形的面积;
(2)若n=5,求所有矩形的面积和;
(3)当分为n等分时,你能用含有n的表达式表示所有矩形的面积和吗?
如图,小红作出了边长为1的第1个正△A1B1C1,算出了正△A1B1C1的面积,然后分别取△A1B1C1三边的中点A2,B2,C2,作出了第2个正△A2B2C2,算出了正△A2B2C2的面积,用同样的方法,作出了第3个正△A3B3C3,算出了正△A3B3C3的面积…,由此可得,第2014个正△A2014B2014C2014的面积是( )

A. |
B. |
C. |
D. |
如图,在Rt△ABC中,∠ACB=90°,AC=8,BC=6,CD⊥AB于点D.点P从点D出发,沿线段DC向点C运动,点Q从点C出发,沿线段CA向点A运动,两点同时出发,速度都为每秒1个单位长度,当点P运动到C时,两点都停止.设运动时间为t秒.
(1)求线段CD的长;
(2)当t为何值时,△CPQ与△ABC相似?
(3)当t为何值时,△CPQ为等腰三角形?
如图,在矩形ABCD中,E是AD边的中点,BE⊥AC于点F,连接DF,分析下列五个结论:①△AEF∽△CAB;②CF=2AF;③DF=DC;④tan∠CAD= ;⑤S四边形CDEF=
;⑤S四边形CDEF= S△ABF,其中正确的结论有 个.
S△ABF,其中正确的结论有 个.

如图,在钝角三角形ABC中,AB=6cm,AC=12cm,动点D从A点出发到B点止,动点E从C点出发到A点止.点D运动的速度为1cm/秒,点E运动的速度为2cm/秒.如果两点同时运动,那么当以点A、D、E为顶点的三角形与△ABC相似时,运动的时间是( )

A.3秒或4.8秒 B.3秒
C.4.5秒 D.4.5秒或4.8秒
阅读:如图1,在△ABC中,BE是AC边上的中线, D是BC边上的一点,CD:BD=1:2,AD与BE相交于点P,求 的值.小昊发现,过点A作AF∥BC,交BE的延长线于点F,通过构造△AEF,经过推理和计算能够使问题得到解决(如图2).
的值.小昊发现,过点A作AF∥BC,交BE的延长线于点F,通过构造△AEF,经过推理和计算能够使问题得到解决(如图2).


(1) 的值为 ;
的值为 ;
(2)参考小昊思考问题的方法,解决问题:
如图3,在△ABC中,∠ACB=90°,点D在BC的延长线上,AD与AC边上的中线BE的延长线交于点P,DC:BC:AC=1:2:3.

 求
求 的值;
的值;
 若CD=2,求BP的长.
若CD=2,求BP的长.