如图,在等腰三角形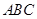 中,
中, ,
,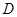 是
是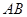 边上一点,以
边上一点,以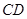 为一边,向上作等腰
为一边,向上作等腰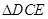 ,使
,使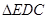 ∽
∽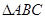 ,连
,连 ,
,
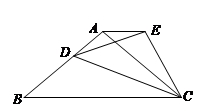
求证:(1)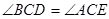 (2)
(2)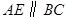
如图是 的网格,正方形网格中的每个小正方形的边长都是,每个小正方形的顶点叫做格点,以格点为顶点的三角形叫格点三角形
的网格,正方形网格中的每个小正方形的边长都是,每个小正方形的顶点叫做格点,以格点为顶点的三角形叫格点三角形
(1)图1中的格点 与
与 相似吗?请说明理由.
相似吗?请说明理由.
(2)请在图2中画一个格点 与
与 相似(注意:
相似(注意: 与
与 、
、 都不全等)
都不全等)
如图:小明想测量一棵树的高度AB,在阳光下,小明测得一根与地面垂直、长为1米的竹竿的影长为0.8米.同时另一名同学测量一棵树的高度时,发现树的影子不全落在地面上,有一部分影子落在教学楼的墙壁上(如图),墙壁上的影长CD为1.5米,落在地面上的影长BD为3米,则树高AB为多少米.

如图,在同一平面内,将两个全等的等腰直角三角形ABC和AFG摆放在一起,A为公共顶点,∠BAC=∠AGF=90°,它们的斜边长为2,若∆ABC固定不动,∆AFG绕点A旋转,AF、AG与边BC的交点分别为D、E(点D不与点B重合,点E不与点C重合),设BE=m,CD=n.
(1)请在图中找出两对相似而不全等的三角形,并选取其中一对进行证明.
(2)求m与n的函数关系式,直接写出自变量n的取值范围.
(3)以∆ABC的斜边BC所在的直线为x轴,BC边上的高所在的直线为y轴,建立平面直角坐标系(如图12).在边BC上找一点D,使BD=CE,求出D点的坐标,并通过计算验证BD +CE
+CE =DE
=DE .
.
(4)在旋转过程中,(3)中的等量关系BD +CE
+CE =DE
=DE 是否始终成立,若成立,请证明,若不成立,请说明理由.
是否始终成立,若成立,请证明,若不成立,请说明理由.
如图,已知AC,EC分别为正方形ABCD和正方形EFCG的对角线,点E在△ABC内,连接BF,∠CAE+∠CBE=90°.
(1)求证:△CAE∽△CBF;
(2)若BE=1,AE=2,求CE的长.
如图,△ABC中,CD是边AB上的高,且 .
.
(1)求证:△ACD∽△CBD;
(2)求∠ACB的大小.
如图,小明同学用自制的直角三角形纸板DEF测量树的高度AB,他调整自己的位置,设法使斜边DF保持水平,并且边DE与点B在同一直线上,已知纸板的两条直角边DE=40cm,EF=20cm,测得边DF离地面的高度AC=1.5m,CD=8m,求树高AB.
如图,DE∥BC,EF∥CG,AD:AB=1:3,AE=3.
(1)求EC的值;
(2)求证:AD•AG=AF•AB.
阅读理解:如图①,在四边形ABCD的边AB上任取一点E(点E不与A、B重合),分别连接ED、EC,可以把四边形ABCD分成三个三角形,如果其中有两个三角形相似,我们就把E叫做四边形ABCD的边AB上的“相似点”;如果这三个三角形都相似,我们就把E叫做四边形ABCD的边AB上的“强相似点”.解决问题:
(1)如图①,∠A=∠B=∠DEC=45°,试判断点E是否是四边形ABCD的边AB上的相似点,并说明理由;
(2)如图②,在矩形ABCD中,A、B、C、D四点均在正方形网格(网格中每个小正方形的边长为1)的格点(即每个小正方形的顶点)上,试在图②中画出矩形ABCD的边AB上的强相似点;
(3)如图③,将矩形ABCD沿CM折叠,使点D落在AB边上的点E处,若点E恰好是四边形ABCM的边AB上的一个强相似点,试探究AB与BC的数量关系.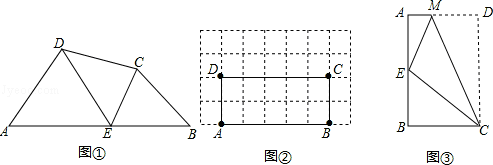
如图,在正方形ABCD中,E为边AD的中点,且DF:CF=1:3,连接EF并延长交BC的延长线于点G,
(1)求证:△ABE∽△DEF;
(2)若正方形的边长为4,求BG的长.
如图1,四边形ABCD中,AD∥BC,∠A=90°,BD⊥CD,AD=
 ,BC=5
,BC=5 ,动点P从点D出发,以1cm/s的速度沿DB方向运动,动点Q也从点D出发,以
,动点P从点D出发,以1cm/s的速度沿DB方向运动,动点Q也从点D出发,以
 /
/ 的速度沿DC方向运动,P,Q两点同时出发,当点Q到达点C时停止运动,点P也随之停止,设运动时间为
的速度沿DC方向运动,P,Q两点同时出发,当点Q到达点C时停止运动,点P也随之停止,设运动时间为
 (
( >0).
>0).
(1)求线段DB的长;
(2)请判断PQ与BC的位置关系,并加以证明;
(3)伴随P,Q两点的运动,将△DPQ绕点P旋转,得到△PMN,点M落在线段PQ上,若△PMN
与△DBC的重叠部分的图形周长为y,
①请求出y与 之间的函数关系式,并指出自变量
之间的函数关系式,并指出自变量 的取值范围;
的取值范围;
②求出当4<y≤5时 的取值范围.
的取值范围.