初中数学相似多边形的性质解答题

在平面直角坐标系xOy中，已知动点P在正比例函数y = x的图象上，点P的横坐标为m （m > 0）．以点P为圆心，m为半径的圆交x轴于A、B两点（点A在点B的左侧），交y轴于C、D两点（D点在点C的上方）．点E为平行四边形DOPE的顶点（如图）．

（1）直接写出点B、E的坐标（用含m的代数式表示）；
（2）连接DB、BE，设△BDE的外接圆交y轴于点Q （点Q异于点D），连接EQ、BQ．试问线段BQ与线段EQ的长是否相等？为什么？
（3）连接BC，求∠DBC −∠DBE的度数．

如图，已知AB是⊙O的弦，OB = 2，∠B = 30°，C是弦AB上任意一点（不与点A、B重合），连接CO并延长CO交⊙O于点D，连接AD．

（1）弦长AB = ____________（结果保留根号）；
（2）当∠D = 20°时，求∠BOD的度数；
（3）当AC的长度为多少时，以点A、C、D为顶点的三角形与以B、C、O为顶点的三角形相似？请写出解答过程．

如图，△ABC中，CD是边AB上的高，且．

（1）求证：△ACD∽△CBD；
（2）求∠ACB的大小．

如图，D为等边△ABC边BC上一点，DE⊥AB于E，若BD∶CD = 2∶1，DE =，求AE．

点A、B、C在同一直线上，在直线AC的同侧作△ABE和△BCF，连接AF，CE．取AF、CE的中点M、N，连接BM，BN，MN．
（1）若△ABE和△FBC是等腰直角三角形，且∠ABE=∠FBC=90°（图1），则△MBN是______三角形；
（2）在△ABE和△BCF中，若BA=BE，BC=BF，且∠ABE=∠FBC=α，（图2），则△MBN是______三角形，且∠MBN=______；
（3）若将（2）中的△ABE绕点B旋转一定角度，（图3），其他条件不变，那么（2）中的结论是否成立？若成立，给出你的证明；若不成立，写出正确的结论并给出证明．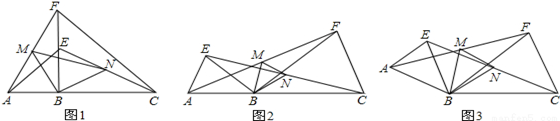

如图，已知在Rt△ABC中，∠ACB=90°，AC=6，BC=8，BE平分∠ABC交AC于点E，EF⊥AB，垂足为F．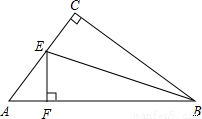

（1）求EF的长度；
（2）作CD⊥AB，垂足为D，CD与BE相交于G，试说明：CE=CG

如图，在Rt△ABC中，∠ACB＝90°，AC＝8，BC＝6，CD⊥AB于点D．点P从点D出发，沿线段DC向点C运动，点Q从点C出发，沿线段CA向点A运动，两点同时出发，速度都为每秒1个单位长度，当点P运动到C时，两点都停止．设运动时间为t秒．

（1）求线段CD的长；
（2）当t为何值时，△CPQ与△ABC相似？
（3）当t为何值时，△CPQ为等腰三角形？

如图，在菱形ABCD中，AB＝4，∠BAD＝120°，△AEF为正三角形，点E、F分别在菱形的边BC、CD上滑动，且E、F不与B、C、D重合．

（1）证明：BE＝CF；
（2）当点E、F在BC、CD上滑动时，四边形AECF面积是否发生变化？如果不变，求出这个定值；
（3）设BE＝x，△CEF的面积为y，求y与x之间的函数关系式（不写出自变量x取值范围）．

如图，在直角坐标系中，直线与轴，轴分别交于两点，以为边在第二象限内作矩形，使．

（1）求点，点的坐标；
（2）过点作轴，垂足为，求证：；
（3）求点的坐标．

已知：△ABC在直角坐标平面内，三个顶点的坐标分别为A（0，3）、B（3，4）、C（2，2）（正方形网格中每个小正方形的边长是一个单位长度）．

（1）画出△ABC向下平移4个单位长度得到的△A₁B₁C₁，点C₁的坐标是           ；
（2）以点B为位似中心，在网格内画出△A₂B₂C₂，使△A₂B₂C₂与△ABC位似，且位似比为2：1，点C₂的坐标是             ；
（3）△A₂B₂C₂的面积是              平方单位．

已知：ΔABC在坐标平面内，三个顶点的坐标为A（0，3）、B（3，4）、C（2，2），（正方形网格中，每个小正方形边长为1个单位长度）

（1）画出ΔABC向下平移4个单位得到的ΔA₁B₁C₁．
（2）以B为位似中心，在网格中画出ΔA₂BC₂，使ΔA₂BC₂与ΔABC位似，且位似比2 ：1，直接写出C₂点坐标是               ．
（3）ΔA₂BC₂的面积是               平方单位．

（1）如图1，在△ABC中，点D、E、Q分别在AB、AC、BC上，且DE∥BC，AQ交DE于点P，求证：；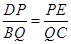
（2）如图，△ABC中，∠BAC=90°，正方形DEFG的四个顶点在△ABC的边上，连接AG，AF分别交DE于M，N两点．
①如图2，若AB=AC=1，直接写出MN的长；
②如图3，求证：MN²=DM·EN．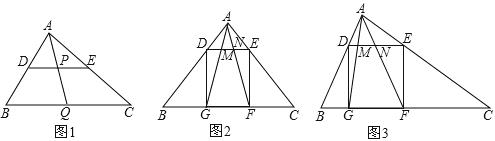

某社区拟筹资金2000元，计划在一块上、下底分别是10米、20米的梯形空地上种植花木（如图所示），他们想在△AMD和△BMC地带种植单价为10元/米²的太阳花，当△AMD地带种满花后，已经花了500元，请你预算一下，若继续在△BMC地带种植同样的太阳花，资金是否够用？并说明理由．

如图，铁道口的栏杆短臂长1米，长臂长16米，当短臂的端点下降0．5米时，求长臂端点应升高了多少米？

李华晚上在两站相距50m的路灯下来回散步，DF=50m．已知李华身高AB=1．7m，灯柱CD=EF=8．5m．

（1）若李华距灯柱CD的距离为DB=xm，他的影子BQ=ym，求y关于x的函数关系式．
（2）若李华在两路灯之间行走，则他前后两个影子PB+BQ是否会发生变化？请说明理由．