在平面直角坐标系xOy中,已知动点P在正比例函数y = x的图象上,点P的横坐标为m (m > 0).以点P为圆心,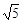 m为半径的圆交x轴于A、B两点(点A在点B的左侧),交y轴于C、D两点(D点在点C的上方).点E为平行四边形DOPE的顶点(如图).
m为半径的圆交x轴于A、B两点(点A在点B的左侧),交y轴于C、D两点(D点在点C的上方).点E为平行四边形DOPE的顶点(如图).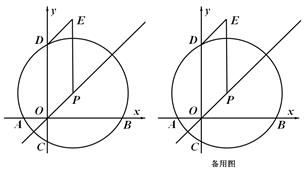
(1)直接写出点B、E的坐标(用含m的代数式表示);
(2)连接DB、BE,设△BDE的外接圆交y轴于点Q (点Q异于点D),连接EQ、BQ.试问线段BQ与线段EQ的长是否相等?为什么?
(3)连接BC,求∠DBC −∠DBE的度数.
推荐套卷
在平面直角坐标系xOy中,已知动点P在正比例函数y = x的图象上,点P的横坐标为m (m > 0).以点P为圆心,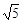 m为半径的圆交x轴于A、B两点(点A在点B的左侧),交y轴于C、D两点(D点在点C的上方).点E为平行四边形DOPE的顶点(如图).
m为半径的圆交x轴于A、B两点(点A在点B的左侧),交y轴于C、D两点(D点在点C的上方).点E为平行四边形DOPE的顶点(如图).
(1)直接写出点B、E的坐标(用含m的代数式表示);
(2)连接DB、BE,设△BDE的外接圆交y轴于点Q (点Q异于点D),连接EQ、BQ.试问线段BQ与线段EQ的长是否相等?为什么?
(3)连接BC,求∠DBC −∠DBE的度数.