如图,Rt△ABC中,O为坐标原点,∠AOB=90°,∠B=30°,如果点A在反比例函数 (x>0)的图象上运动,那么点B在函数(填函数解析式)的图象上运动.
(x>0)的图象上运动,那么点B在函数(填函数解析式)的图象上运动.
如图,在函数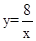 (x>0)的图象上有点P1、P2、P3…、Pn、Pn+1,点P1的横坐标为2,且后面每个点的横坐标与它前面相邻点的横坐标的差都是2,过点P1、P2、P3…、Pn、Pn+1分别作x轴、y轴的垂线段,构成若干个矩形,如图所示,将图中阴影部分的面积从左至右依次记为S1、S2、S3…、Sn,则S1= _______ ,Sn= _________ .(用含n的代数式表示)
(x>0)的图象上有点P1、P2、P3…、Pn、Pn+1,点P1的横坐标为2,且后面每个点的横坐标与它前面相邻点的横坐标的差都是2,过点P1、P2、P3…、Pn、Pn+1分别作x轴、y轴的垂线段,构成若干个矩形,如图所示,将图中阴影部分的面积从左至右依次记为S1、S2、S3…、Sn,则S1= _______ ,Sn= _________ .(用含n的代数式表示)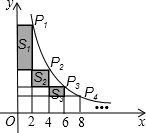
如图,反比例函数y= (x>0)的图象和矩形ABCD在第一象限,AD∥x轴,且AB=2,AD=4,点A的坐标为(2,6).若将矩形向下平移,使矩形的两个顶点恰好同时落在反比例函数的图象上,则k的值是.
(x>0)的图象和矩形ABCD在第一象限,AD∥x轴,且AB=2,AD=4,点A的坐标为(2,6).若将矩形向下平移,使矩形的两个顶点恰好同时落在反比例函数的图象上,则k的值是.
如图1~4所示,每个图中的“7”字形是由若干个边长相等的正方形拼接而成,“7”字形的一个顶点 落在反比例函数
落在反比例函数 的图像上,另“7”字形有两个顶点落在
的图像上,另“7”字形有两个顶点落在 轴上,一个顶点落在
轴上,一个顶点落在 轴上.
轴上.
(1)图1中的每一个小正方形的面积是;
(2)按照图1 图2
图2 图3
图3 图4
图4
 这样的规律拼接下去,第
这样的规律拼接下去,第 个图形中每一个小正方形的面积是.(用含
个图形中每一个小正方形的面积是.(用含 的代数式表示)
的代数式表示)
如图,A、B是第二象限内双曲线y= 上的点,A、B两点的横坐标分别是a、2a,线段AB的延长线交x轴于点C,若S△AOC=6,则k的值为.
上的点,A、B两点的横坐标分别是a、2a,线段AB的延长线交x轴于点C,若S△AOC=6,则k的值为.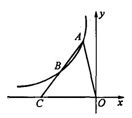
以下四个命题:
①每一条对角线都平分一组对角的平行四边形是菱形.
②当m > 0时, y =–mx+1与 两个函数都是y随着x的增大而减小.
两个函数都是y随着x的增大而减小.
③已知正方形的对称中心在坐标原点,顶点A,B,C,D按逆时针依次排列,若A点坐标为(1, )则D点坐标为(1,
)则D点坐标为(1, ).
).
④在一个不透明的袋子中装有标号为1,2,3,4的四个完全相同的小球,从袋中随机摸取一个然后放回,再从袋中随机地摸取一个,则两次取到的小球标号的和等于4的概率为 .
.
其中正确的命题有(只需填正确命题的序号)
如图,点P1(x1,y1),点P2(x2,y2),…,点Pn(xn,yn)都在函数 (x>0)的图象上,△P1OA1,△P2A1A2,△P3A2A3,…,△PnAn﹣1An都是等腰直角三角形,斜边OA1,A1A2,A2A3,…,An﹣1An都在x轴上(n是大于或等于2的正整数),已知点A1的坐标为(2,0),则点P1的坐标为 ;点P2的坐标为 ;点Pn的坐标为 (用含n的式子表示).
(x>0)的图象上,△P1OA1,△P2A1A2,△P3A2A3,…,△PnAn﹣1An都是等腰直角三角形,斜边OA1,A1A2,A2A3,…,An﹣1An都在x轴上(n是大于或等于2的正整数),已知点A1的坐标为(2,0),则点P1的坐标为 ;点P2的坐标为 ;点Pn的坐标为 (用含n的式子表示).
如图,若双曲线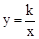 与边长为5的等边△AOB的边OA、AB分别相交于C、D两点,且OC=3BD,则实数k的值为.
与边长为5的等边△AOB的边OA、AB分别相交于C、D两点,且OC=3BD,则实数k的值为.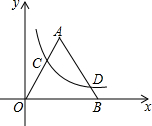
在反比例函数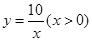 的图象上,有一系列点
的图象上,有一系列点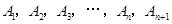 ,若
,若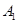 的横坐标为2,且以后每点的横坐标与它前一个点的横坐标的差都为2,现分别过点
的横坐标为2,且以后每点的横坐标与它前一个点的横坐标的差都为2,现分别过点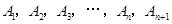 ,作x轴与y轴的垂线段,构成若干个矩形如下图所示,将图中阴影部分的面积从左到右依次记为
,作x轴与y轴的垂线段,构成若干个矩形如下图所示,将图中阴影部分的面积从左到右依次记为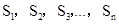 ,则
,则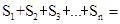 ______.(用n的代数式表示)
______.(用n的代数式表示)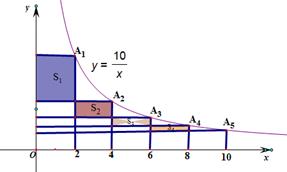
两个反比例函数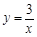 ,
, 在第一象限内的图像如图所示,点
在第一象限内的图像如图所示,点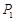 ,
, ,
,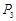 ,…,
,…,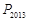 在函数
在函数 的图像上,它们的横坐标分别是
的图像上,它们的横坐标分别是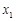 ,
, ,
, ,…,
,…,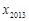 ,纵坐标分别是1,3,5,…,共2013个连续奇数,过点
,纵坐标分别是1,3,5,…,共2013个连续奇数,过点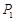 ,
, ,
,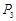 ,…,
,…,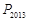 分别作y轴的平行线,与函数
分别作y轴的平行线,与函数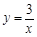 的图像交点依次是
的图像交点依次是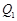 (
(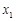 ,
,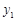 ),
),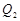 (
( ,
,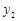 ),
),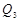 (
( ,
,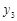 ),…,
),…, (
(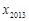 ,
,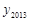 ),则
),则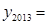 .
.
如图,M为双曲线y=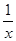 上的一点,过点M作x轴、y轴的垂线,分别交直线y=-x+m于D、C两点,若直线y=-x+m与y轴交于点A,与x轴相交于点B,则AD·BC的值为.
上的一点,过点M作x轴、y轴的垂线,分别交直线y=-x+m于D、C两点,若直线y=-x+m与y轴交于点A,与x轴相交于点B,则AD·BC的值为.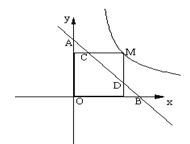
如图,点A在双曲线y=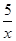 上,点B在双曲线y=
上,点B在双曲线y=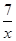 上,且AB∥x轴,C、D在x轴上,若四边形ABCD为平行四边形,则它的面积为.
上,且AB∥x轴,C、D在x轴上,若四边形ABCD为平行四边形,则它的面积为.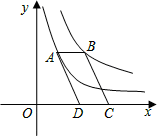
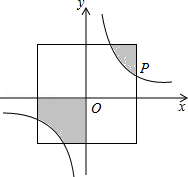
如图,在直角坐标系中,正方形的中心在原点O,且正方形的一组对边与x轴平行,点P(3a,a)是反比例函数y=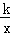 (k>0)的图象上与正方形的一个交点.若图中阴影部分的面积等于9,则这个反比例函数的解析式为_________ .
(k>0)的图象上与正方形的一个交点.若图中阴影部分的面积等于9,则这个反比例函数的解析式为_________ .