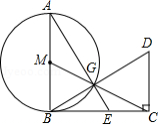
如图, 是 的直径, 是 的切线,切点为 , 是 上(除 点外)的任意一点,连接 交 于点 ,过点 作 交 的延长线于点 ,连接 并延长交 于点 .
(1)求证: ;
(2)若 ,求 的长度.
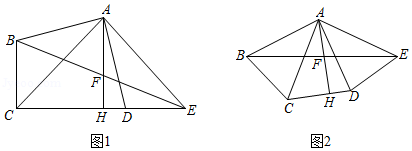
已知四边形ABCD中, ,连接AC,过点A作 ,且使 ,连接BE,过A作 于H交BE于F.
(1)如图1,当E在CD的延长线上时,求证: ; ;
(2)如图2,当E不在CD的延长线上时,BF=EF还成立吗?请证明你的结论.
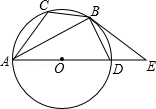
如图,已知⊙O是△ABC的外接圆,AD是⊙O的直径,且 ,延长AD到E,且有 .
(1)求证:BE是⊙O的切线;
(2)若 , ,求圆的直径AD及切线BE的长.
如图,在△ ABC中, D、 E分别为 AB、 AC边上的点, , BE与 CD相交于点 F,则下列结论一定正确的是( )

| A. |
|
B. |
|
C. |
|
D. |
|
如图,在△ ABC中,点 D是 AB边上的一点.
(1)请用尺规作图法,在△ ABC内,求作∠ ADE,使∠ ADE=∠ B, DE交 AC于 E;(不要求写作法,保留作图痕迹)
(2)在(1)的条件下,若 =2,求 的值.

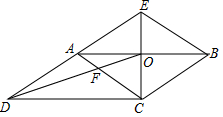
如图, CE是▱ ABCD的边 AB的垂直平分线,垂足为点 O, CE与 DA的延长线交于点 E.连接 AC, BE, DO, DO与 AC交于点 F,则下列结论:
①四边形 ACBE是菱形;
②∠ ACD=∠ BAE;
③ AF: BE=2:3;
④ S 四边形 AFOE: S △ COD=2:3.
其中正确的结论有 .(填写所有正确结论的序号)
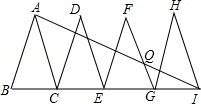
如图,已知△ABC、△DCE、△FEG、△HGI是4个全等的等腰三角形,底边BC、CE、EG、GI在同一直线上,且AB=2,BC=1,连接AI,交FG于点Q,则QI= .
如图, 已知正方形  ,点
,点 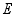 是
是 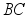 边的中点,
边的中点,  与
与 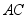 相交于点
相交于点 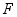 ,连接
,连接 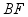 ,下列结论:①
,下列结论:① 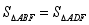 ;②
;②  ;③
;③ 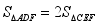 ;④
;④  ,其中正确的是
,其中正确的是 

| A. |
A .①③B .②③C .①④D .②④ |
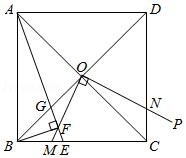
如图,在正方形 中,对角线 , 相交于点 ,点 在 边上,且 ,连接 交 于点 ,过点 作 于点 ,连接 并延长,交 于点 ,过点 作 交 于点 , ,现给出下列结论:① ;② ;③ ;④ ;其中正确的结论有
| A. |
①②③ |
B. |
②③④ |
C. |
①②④ |
D. |
①③④ |