初中数学黄金分割试题

如图，乐器上一根弦固定在乐器面板上A、B两点，支撑点C是靠近点B的黄金分割点，若AB＝10cm，则AC＝______________cm．（结果精确到0.1）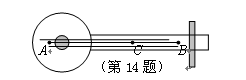

古希腊数学家欧多克索斯在深入研究比例理论时，提出了分线段的“中末比”问题：点 $G$将一线段 $\mathit{MN}$分为两线段 $\mathit{MG}$， $\mathit{GN}$，使得其中较长的一段 $\mathit{MG}$是全长 $\mathit{MN}$与较短的一段 $\mathit{GN}$的比例中项，即满足 $\frac{\mathit{MG}}{\mathit{MN}}=\frac{\mathit{GN}}{\mathit{MG}}=\frac{\sqrt{5}-1}{2}$，后人把 $\frac{\sqrt{5}-1}{2}$这个数称为“黄金分割”数，把点 $G$称为线段 $\mathit{MN}$的“黄金分割”点．如图，在 $\mathit{\Delta ABC}$中，已知 $\mathit{AB}=\mathit{AC}=3$， $\mathit{BC}=4$，若 $D$， $E$是边 $\mathit{BC}$的两个“黄金分割”点，则 $\mathit{\Delta ADE}$的面积为 $($　　 $)$

A． $10-4\sqrt{5}$B． $3\sqrt{5}-5$C． $\frac{5-2\sqrt{5}}{2}$D． $20-8\sqrt{5}$

再读教材：

宽与长的比是 $\frac{\sqrt{5}-1}{2}$（约为 $0.618)$的矩形叫做黄金矩形，黄金矩形给我们以协调、匀称的美感，世界各国许多著名的建筑，为取得最佳的视觉效果，都采用了黄金矩形的设计，下面，我们用宽为2的矩形纸片折叠黄金矩形．（提示： $\mathit{MN}=2)$

第一步，在矩形纸片一端，利用图①的方法折出一个正方形，然后把纸片展平．

第二步，如图②，把这个正方形折成两个相等的矩形，再把纸片展平．

第三步，折出内侧矩形的对角线 $\mathit{AB}$，并把 $\mathit{AB}$折到图③中所示的 $\mathit{AD}$处．

第四步，展平纸片，按照所得的点 $D$折出 $\mathit{DE}$，使 $\mathit{DE}\perp \mathit{ND}$，则图④中就会出现黄金矩形．

问题解决：

（1）图③中 $\mathit{AB}=$　　（保留根号）；

（2）如图③，判断四边形 $\mathit{BADQ}$的形状，并说明理由；

（3）请写出图④中所有的黄金矩形，并选择其中一个说明理由．

实际操作

（4）结合图④，请在矩形 $\mathit{BCDE}$中添加一条线段，设计一个新的黄金矩形，用字母表示出来，并写出它的长和宽．

如图，在 $\mathit{\Delta ABC}$中， $\angle B=\angle C=36°$， $\mathit{AB}$的垂直平分线交 $\mathit{BC}$于点 $D$，交 $\mathit{AB}$于点 $H$， $\mathit{AC}$的垂直平分线交 $\mathit{BC}$于点 $E$，交 $\mathit{AC}$于点 $G$，连接 $\mathit{AD}$， $\mathit{AE}$，则下列结论错误的是 $($　　 $)$

A． $\frac{\mathit{BD}}{\mathit{BC}}=\frac{\sqrt{5}-1}{2}$B． $\mathit{AD}$， $\mathit{AE}$将 $\angle \mathit{BAC}$三等分

C． $\mathit{\Delta ABE}\cong \mathit{\Delta ACD}$D． $S_{\mathit{\Delta ADH}}=S_{\mathit{\Delta CEG}}$

实数 $a$， $n$， $m$， $b$满足 $a<n<m<b$，这四个数在数轴上对应的点分别为 $A$， $N$， $M$， $B$（如图），若 $A{M}^2=\mathit{BM}\cdot \mathit{AB}$， $B{N}^2=\mathit{AN}\cdot \mathit{AB}$，则称 $m$为 $a$， $b$的“大黄金数”， $n$为 $a$， $b$的“小黄金数”，当 $b-a=2$时， $a$， $b$的大黄金数与小黄金数之差 $m-n=$　　．

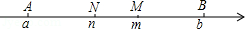
生活中到处可见黄金分割的美．如图，在设计人体雕像时，使雕像的腰部以下 $a$ 与全身 $b$ 的高度比值接近0.618，可以增加视觉美感．若图中 $b$ 为2米，则 $a$ 约为 $($ 　　 $)$

A．

1.24米

B．

1.38米

C．

1.42米

D．

1.62米

如图，在矩形中，，，点在上，将沿折叠，点恰好落在对角线上的点，为上一点，经过点，

（1）求证：是的切线；

（2）在边上截取，点是线段的黄金分割点吗？请说明理由．

黄金分割数 $\frac{\sqrt{5}-1}{2}$ 是一个很奇妙的数，大量应用于艺术、建筑和统计决策等方面，请你估算 $\sqrt{5}-1$ 的值 $($ 　　 $)$

A．	在1.1和1.2之间	B．	在1.2和1.3之间
C．	在1.3和1.4之间	D．	在1.4和1.5之间

宽与长的比是 $\frac{\sqrt{5}-1}{2}$ （约 $0.618)$ 的矩形叫做黄金矩形，黄金矩形蕴藏着丰富的美学价值，给我们以协调和匀称的美感．我们可以用这样的方法画出黄金矩形：作正方形 $\mathit{ABCD}$ ，分别取 $\mathit{AD}$ 、 $\mathit{BC}$ 的中点 $E$ 、 $F$ ，连接 $\mathit{EF}$ ：以点 $F$ 为圆心，以 $\mathit{FD}$ 为半径画弧，交 $\mathit{BC}$ 的延长线于点 $G$ ；作 $\mathit{GH}\perp \mathit{AD}$ ，交 $\mathit{AD}$ 的延长线于点 $H$ ，则图中下列矩形是黄金矩形的是 $($ 　　 $)$

A．

矩形 $\mathit{ABFE}$

B．

矩形 $\mathit{EFCD}$

C．

矩形 $\mathit{EFGH}$

D．

矩形 $\mathit{DCGH}$

如图，已知的中垂线交于点，交于点，有下面3个结论：

①是等腰三角形；
②∽；
③点D是线段AC的黄金分割点．
请你从以上结论中只选一个加以证明

如图，点C为线段AB上的一点，AC>BC，已知AB=10，若点C为线段AB的黄金分割点，则BC=______________．