初中数学坐标与图形变化-旋转试题

如图，所有正三角形的一边平行于x轴，一顶点在y轴上．从内到外，它们的边长依次为2,4,6,8，…，顶点依次用表示，其中x轴与边，边与，与，…均相距一个单位，则顶点的坐标为；的坐标为；（n为正整数）的坐标为．

如图，把一个矩形纸片OABC放入平面直角坐标系中，使OA、OC分别落在x轴、y轴上，连接OB，将纸片OABC沿OB折叠，使点A落在A′的位置上．若OB=,,则点A′的坐标．

如图，点B在x轴上，∠ABO=90°，∠A=30°，OA=4，将△OAB饶点O按顺时针方向旋转120°得到△OA′B′，则点A′的坐标是（　　）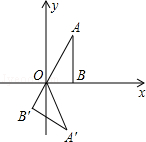

A．（2，﹣2）

B．（2，﹣2）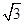

C．（2，﹣2）

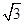D．（2，﹣2）

如图，在平面直角坐标系中，点A、B的坐标分别为（-5，0）和（5，0），以AB为直径在x轴的上方作半圆O，点C是该半圆上第一象限内的一个动点，连结AC、BC，并延长BC至点D，使BC=CD，过点D作x轴的垂线，分别交x轴、线段AC于点E、F，E为垂足，连结OF．

（1）当∠CAB=30°时，求弧BC的长；
（2）当AE=6时，求弦BC的长；
（3）在点C运动的过程中，是否存在以点O、E、F为顶点的三角形与△DEB相似？若存在，请求出此时E点的坐标；若不存在，请说明理由．

如图，在平面直角坐标系中，Rt△OAB的顶点A在x轴的正半轴上，顶点B的坐标为（3，），点C的坐标为（1，0），点P为斜边OB上的一动点，则△PAC周长的最小值为

已知下面是3个5×5的正方形网格，小正方形边长都为1，A、B两点在小网格的顶点上，位置如图所示．现请你分别在三个网格中各画一个△ABC．要求：

（1）顶点C在网格的顶点上；
（2）工具只用无刻度的直尺；
（3）所画的3个三角形互不全等，但面积都为2.

如图1，在平面直角坐标系内，已知点，，，，记线段为，线段为，点是坐标系内一点．给出如下定义：若存在过点的直线l与，都有公共点，则称点是联络点．
例如，点是联络点．
（1）以下各点中，__________________是联络点（填出所有正确的序号）；
①；②；③．
（2）直接在图1中画出所有联络点所组成的区域，用阴影部分表示；
（3）已知点M在y轴上，以M为圆心，r为半径画圆，⊙M上只有一个点为联络点，
①若，求点M的纵坐标；
②求r的取值范围．

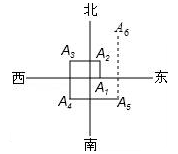
如图，正方形A₁A₂A₃A₄，A₅A₆A₇A₈，A₉A₁₀A₁₁A₁₂，…，（每个正方形从第三象限的顶点开始，按顺时针方向顺序，依次记为A₁，A₂，A₃，A₄；A₅，A₆，A₇，A₈；A₉，A₁₀，A₁₁，A₁₂；…）的中心均在坐标原点O，各边均与x轴或y轴平行，若它们的边长依次是2，4，6…，则顶点A₂₀的坐标为．

在平面直角坐标系xOy中，设点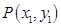，是图形W上的任意两点．
定义图形W的测度面积：若的最大值为m，的最大值为n，则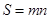为图形W的测度面积．
例如，若图形W是半径为1的⊙O．当P，Q分别是⊙O与x轴的交点时，如图1，取得最大值，且最大值m=2；当P，Q分别是⊙O与y轴的交点时，如图2，取得最大值，且最大值n=2．则图形W的测度面积．

（1）若图形W是等腰直角三角形ABO，OA=OB=1．
①如图3，当点A，B在坐标轴上时，它的测度面积S=；
②如图4，当AB⊥x轴时，它的测度面积S=；
（2）若图形W是一个边长为1的正方形ABCD，则此图形测度面积S的最大值为；
（3）若图形W是一个边长分别为3和4的矩形ABCD，求它的测度面积S的取值范围．

在平面直角坐标系中，规定把一个三角形先沿着x轴翻折，再向右平移2个单位称为1次变换.如图，已知等边三角形ABC的顶点B，C的坐标分别是（－1，－1），（－3，－1），把△ABC经过连续9次这样的变换得到△A₉B₉C₉，则点A的对应点A₉的坐标是　　　　.

如图，在平面直角坐标系中，O是原点，已知A（4，3），P是y轴上的动点，当点O,A,P
三点组成的三角形为等腰三角形时，求出所有符合条件的点P坐标．

如图1，在直角坐标系中，点A的坐标为（1，0），以OA为一边在第一象限内作正方形OABC，点D是x轴正半轴上一动点（OD>1，且OD≠2），连接BD，以BD为边在第一象限内作正方形DBFE，设M为正方形DBFE的中心，直线MA交y轴于点N．如果定义：只有一组对角是直角的四边形叫做损矩形．

（1）试找出图1中的一个损矩形 ；
（2）试说明（1）中找出的损矩形一定有外接圆；
（3）随着点D的位置变化，点N的位置是否会发生变化？若没有发生变化，求出点N的坐标；若发生变化，请说明理由．
（4）在图2中，过点M作MG⊥y轴，垂足是点G，连结DN，若四边形DMGN为损矩形，求点D的坐标．

在平面直角坐标系中，已知A（1,1），要在坐标轴上找一点P，使得△PAO为等腰三角形，这样的P点有几个（）

A．9

B．8

C．7

D．6

如图，一个机器人从点O出发，向正东方向走3m到达点A₁，再向正北方向走6m到达点A₂，再向正西方向走9m到达点A₃，再向正南方向走12m到达点A₄，再向正东方向走15m到达点A₅．按如此规律下去，当机器人走到点A₆时，离点O的距离是 m．

如图，在平面直角坐标系中，Rt△OAB的顶点A的坐标为（9，0),，点C的坐标为（2，0），点P为斜边OB上的一个动点，则PA+PC的最小值为_______________.