如图,在平面直角坐标系xOy中,点A(1,0),B(2,0),正六边形ABCDEF沿x轴正方向无滑动滚动,保持上述运动过程,经过(2014,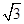 )的正六边形的顶点是()
)的正六边形的顶点是()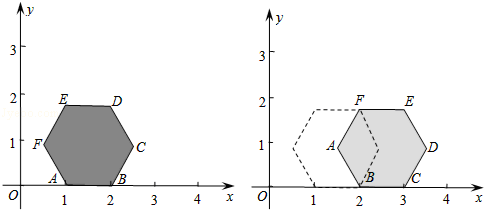
| A.C或E | B.B或D | C.A或E | D.B或F |
(本题14分)在平面直角坐标系中,O为原点,四边形OABC的顶点A在 轴的正半轴上,OA=4,OC=2,点P,点Q分别是边BC,边AB上的点,连结AC,PQ,点B1是点B关于PQ的对称点.
轴的正半轴上,OA=4,OC=2,点P,点Q分别是边BC,边AB上的点,连结AC,PQ,点B1是点B关于PQ的对称点.
(1)若四边形OABC为矩形,如图1,
①求点B的坐标;
②若BQ:BP=1:2,且点B1落在OA上,求点B1的坐标;
(2)若四边形OABC为平行四边形,如图2,且OC⊥AC,过点B1作B1F∥ 轴,与对角线AC、边OC分别交于点E、点F.若B1E: B1F=1:3,点B1的横坐标为
轴,与对角线AC、边OC分别交于点E、点F.若B1E: B1F=1:3,点B1的横坐标为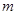 ,求点B1的纵坐标,并直接写出
,求点B1的纵坐标,并直接写出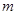 的取值范围.
的取值范围.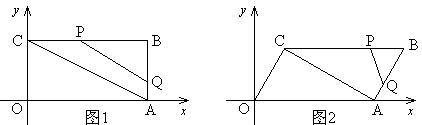
等腰Rt△ABC中,∠BAC=90°,点A、点B分别是x轴、y轴两个动点,直角边AC交x轴于点D,斜边BC交y轴于点E;
(1)如图(1),若A(0,1),B(2,0),求C点的坐标;
(2)如图(2),当等腰Rt△ABC运动到使点D恰为AC中点时,连接DE,求证:∠ADB=∠CDE
(3)如图(3),在等腰Rt△ABC不断运动的过程中,若满足BD始终是∠ABC的平分线,试探究:线段OA、OD、BD三者之间是否存在某一固定的数量关系,并说明理由.
如图,在平面直角坐标系中,O为坐标原点,点A、B的坐标分别为(0,4)、(-3,0),点E、F分别为AB、BO的中点,分别连接AF、EO,交点为P,点P坐标为()
A、(- ,
, ) B、(-
) B、(- ,2) C、(-1,
,2) C、(-1, ) D、(-1,2)
) D、(-1,2)
如图所示,直线BC经过原点O,点A在x轴上,AD⊥BC于D,若B(m,3),C(n,-5),A(4,0),则AD·BC=.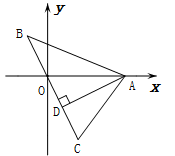
如图,以直角三角形AOC的直角顶点O为原点,以OC、OA所在直线为x轴和y轴建立平面直角坐标系,点A(0, a),C(b,0)满足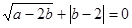 。
。
(1)则C点的坐标为__________;A点的坐标为__________.
(2)已知坐标轴上有两动点P、Q同时出发,P点从C点出发沿x轴负方向以1个单位长度每秒的速度匀速移动,Q点从O点出发以2个单位长度每秒的速度沿y轴正方向移动,点Q到达A点整个运动随之结束.AC的中点D的坐标是(1,2),设运动时间为t(t>0)秒.问:是否存在这样的t,使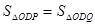 ,若存在,请求出t的值;若不存在,请说明理由.
,若存在,请求出t的值;若不存在,请说明理由.
(3)点F是线段AC上一点,满足∠FOC=∠FCO, 点G是第二象限中一点,连OG,使得∠AOG=∠AOF.点E是线段OA上一动点,连CE交OF于点H, 当点E在线段OA上运动的过程中,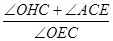 的值是否会发生变化,若不变,请求出它的值;若变化,请说明理由.
的值是否会发生变化,若不变,请求出它的值;若变化,请说明理由.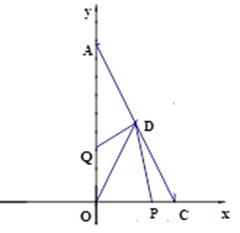
如图,点O(0,0),A(0,1)是正方形OAA1B的两个顶点,以OA1对角线为边作正方形OA1A2B1,再以正方形的对角线OA2作正方形OA1A2B1,…,依此规律,则点A8的坐标是()
| A.(﹣8,0) | B.(0,8) | C.(0,8 ) ) |
D.(0,16) |
如图,在平面直角坐标系中,有若干个横纵坐标分别为整数的点,其顺序按图中“→”方向排列,如(1,0),(2,0),(2,1),(1,1)(1,2),(2,2),…,根据这个规律,第2015个点的坐标为 .
在平面直角坐标系中,A(2,0)、B(0,3),过点B作直线∥x轴,点P(a,3)是直线上的动点,以AP为边在AP右侧作等腰RtAPQ,∠APQ=Rt∠,直线AQ交y轴于点C.
(1)当a=1时,则点Q的坐标为 ;
(2)当点P在直线上运动时,点Q也随之运动.当a= 时,AQ+BQ的值最小为 .
如图,有一块边长为6cm的正三角形纸板,在它的三个角处分别截去一个彼此全等的筝形,再沿图中的虚线折起,做成一个无盖的直三棱柱纸盒,则该纸盒侧面积的最大值是()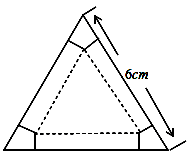
A.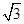 cm2 cm2 |
B. cm2 cm2 |
C.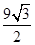 cm2 cm2 |
D.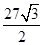 cm2 cm2 |
如图,在平面直角坐标系中,以点B(0,8)为端点的射线BG∥x轴,点A是射线BG上的一个动点(点A与点B不重合).在射线AG上取AD=OB,作线段AD的垂直平分线,垂足为E,且与x轴交于点F,过点A作AC⊥OA,交射线EF于点C.连接OC、CD,设点A的横坐标为t.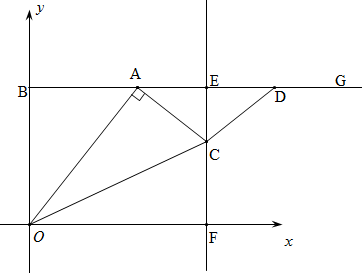
(1)用含t的式子表示点E的坐标为_______;
(2)当t为何值时,∠OCD=180°?
(3)当点C与点F不重合时,设△OCF的面积为S,求S与t之间的函数解析式.
如图1,在直角坐标系中,点A的坐标为(1,0),以OA为一边在第一象限内作正方形OABC,点D是x轴正半轴上一动点(OD>1,且OD≠2),连接BD,以BD为边在第一象限内作正方形DBFE,设M为正方形DBFE的中心,直线MA交y轴于点N.如果定义:只有一组对角是直角的四边形叫做损矩形.
(1)试找出图1中的一个损矩形 ;
(2)试说明(1)中找出的损矩形一定有外接圆;
(3)随着点D的位置变化,点N的位置是否会发生变化?若没有发生变化,求出点N的坐标;若发生变化,请说明理由.
(4)在图2中,过点M作MG⊥y轴,垂足是点G,连结DN,若四边形DMGN为损矩形,求点D的坐标.
如图,在平面直角坐标系中,点A在第一象限,点P在x轴上,若以P,O,A为顶点的三角形是等腰三角形,则满足条件的点P共有()
| A.2个 | B.3个 | C.4个 | D.5个 |