初中数学坐标与图形变化-旋转解答题

做图:在△ABC中，，．

(1)将△向右平移4个单位长度，画出平移后的△；
(2)画出△关于轴对称的△；
(3)将△绕原点O旋转180º，画出旋转后的△；
(4)在△．△．△中，
△       与△        成轴对称，对称轴是          ；
△       与△       成中心对称，对称中心的坐标是         

如图，在直角坐标系中，已知点A（，），点B（，1），平移线段AB，使点A落在A₁（0，），点B落在点B₁，则点B₁的坐标为      ．

在平面直角坐标系中，分别描出点A（-1，0），B（0，2），C（1，0），
D（0，-2）．

试判断四边形ABCD的形状；
若B、D两点不动，你能通过变动点A、C的位置使四边形ABCD成为正方形吗？  若能，请写出变动后的点A、C的坐标．

如图，一只甲虫在.的方格（每小格边长为1）上沿着网格线运动。它从A处出发去看望B、C、D处的其他甲虫。规定：向上、向右走为正，向下、向左走为负。如从A到B记为：（+1，+4），从B到A记为：（-1，-4），括号内第一个数表示左右方向，第二个数表示上下方向，那么图中

（1）填空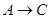：（    ，   4 ），（   ，     ），(  +1  ，—2 ），
（2）若这只甲虫的行走路线为，请计算该甲虫走过的路程；
（3）若这只甲虫从A处去甲虫P处的行走路线一次为（+1，+2），（+2，—1），（—2，+3），（—1，—2），请在图中标出P的位置。

如图，已知的顶点，，是坐标原点．将绕点按逆时针旋转90°得到．

写出两点的坐标；
求过三点的抛物线的解析式，并求此抛物线的顶点的坐标；
在线段上是否存在点使得？若存在，请求出点的坐标；若不存在，请说明理由．

已知△ABC在平面直角坐标系中的位置如图所示．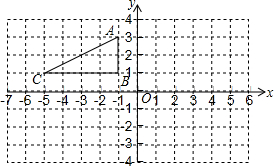

（1）将△ABC绕圆点O旋转180°得到△A₁B₁C₁，请你在图中画出△A₁B₁C₁；
（2）写出点A₁的坐标；
（3）求△A₁B₁C₁的面积．

(满分l2分)如图，已知△ABC的三个顶点的坐标分别为A(-2，-3)，B(-6，0)，C(-1，0)．

(1)请直接写出点A关于x轴对称的点的坐标；
(2)将△ABC绕坐标原点O按逆时针方向旋转90°．画出图形，并直接写出点B的对应点的坐标；
(3)请直接写出：以A，B，C为顶点的平行四边形的第四个顶点D的坐标．

如图, 在平面直角坐标系中, 点(0,8), 点(6 , 8 ).

(1)只用直尺(没有刻度)和圆规, 求作一个点，使点同时满足下列两个条件：(要求保留作图痕迹, 不必写出作法)：
①点P到、两点的距离相等；②点P到的两边的距离相等.
(2) 在(1)作出点后, 在图上写出点的坐标.

如图，A（﹣1，0），C（1，4），点B在x轴上，且AB=3．

（1）求点B的坐标；
（2）求△ABC的面积；
（3）在y轴上是否存在点P，使以A、B、P三点为顶点的三角形的面积为10？若存在，请直接写出点P的坐标；若不存在，请说明理由．

如图，点A从原点出发沿数轴向左运动，同时，点B也从原点出发沿数轴向右运动，3秒后，两点相距15个单位长度．已知点B的速度是点A的速度的4倍（速度单位：单位长度/秒）．

（1）求出点A、点B运动的速度，并在数轴上标出A、B两点从原点出发运动3秒时的位置；
（2）若A、B两点从（1）中的位置开始，仍以原来的速度同时沿数轴向左运动，几秒时，原点恰好处在点A、点B的正中间？
（3）若A、B两点从（1）中的位置开始，仍以原来的速度同时沿数轴向左运动时，另一点C同时从B点位置出发向A点运动，当遇到A点后，立即返回向B点运动，遇到B点后又立即返回向A点运动，如此往返，直到B点追上A点时，C点立即停止运动．若点C一直以20单位长度/秒的速度匀速运动，那么点C从开始运动到停止运动，行驶的路程是多少个单位长度？

已知△ABC各顶点的坐标为A（﹣4，﹣2），B（﹣1，﹣3），C（﹣2，﹣1），将△ABC先向右平移4个单位长度，再向上平移3个单位长度得到△A′B′C′．

（1）在直角坐标系中画出△A′B′C′；
（2）求出△A′B′C′的面积．

画出数轴，在数轴上表示下列各数，并用“<”连接：
-，  ，0 ，

如图，已知火车站的坐标为（2，1），文化宫的坐标为（－1，2）．
（1）请你根据题目条件，画出平面直角坐标系；
（2）写出体育场、市场、超市的坐标．

如图，方格纸中每个小方格都是边长为1个单位长度的正方形，已知点A（-1，1），现将A点先向左平移3个单位，再向下平移4个单位得到点B，然后作点B关于轴的对称点得到C点，最后做点C关于轴的对称点得到D点。
在坐标系中作出点A、B、C、D。
顺次连接ABCDA，求四边形ABCD的面积。

（本小题满分10分）
如图，长方形OABC中，O为平面直角坐标系的原点，点A、C的坐标分别为A（3，0）、
C（0，2），点B在第一象限。

(1)写出点B的坐标；
(2)若过点C的直线交长方形的OA边于点D，且把长方形OABC的周长分成2∶3的两部分，求点D的坐标；
(3)如果将（2）中的线段CD向下平移3个单位长度，得到对应线段C′D′，在平面直角坐标系中画出△CD′C′，并求出它的面积。