在平面直角坐标系中,已知直线经过A(-3,7)、B(2,-3)两点。
(1)求经过A、B两点的一次函数关系式;
(2)画出该一次函数的图象。
如图,在平面直角坐标系中,正方形OABC的边长是2.O为坐标原点,点A在x的正半轴上,点C在y的正半轴上.一条抛物线经过A点,顶点D是OC的中点.

(1)求抛物线的表达式;
(2)正方形OABC的对角线OB与抛物线交于E点,线段FG过点E与x轴垂直,分别交x轴和线段BC于F,G点,试比较线段OE与EG的长度;
(3)点H是抛物线上在正方形内部的任意一点,线段IJ过点H与x轴垂直,分别交x轴和线段BC于I、J点,点K在y轴的正半轴上,且OK=OH,请证明△OHI≌△JKC.
如图,在平面直角坐标系 中,二次函数
中,二次函数 的图象经过点
的图象经过点 ,顶点为
,顶点为 .
.
(1)求这个二次函数的解析式;
(2)若点 的坐标为
的坐标为 ,连接
,连接 ,过点
,过点 作
作 ,垂足为点
,垂足为点 .当点
.当点 在直线
在直线 上,且满足
上,且满足 时,求点
时,求点 的坐标.
的坐标.
如图,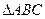 中,
中,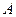 、
、 两点在
两点在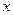 轴的上方,点
轴的上方,点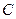 的坐标是(-1,0).以点
的坐标是(-1,0).以点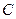 为位似中心,在
为位似中心,在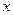 轴的下方作
轴的下方作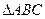 的位似图形
的位似图形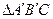 ,并把
,并把 的边长放大到原来的2倍.设点
的边长放大到原来的2倍.设点 的对应点
的对应点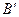 的横坐标是2,求点
的横坐标是2,求点 的横坐标
的横坐标
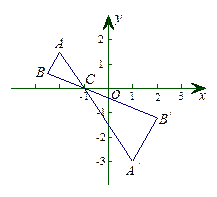
△ABC在平面直角坐标系中的位置如图5所示.
(1)作出与△ABC关于 轴对称的△A1B1C1;
轴对称的△A1B1C1;
(2)写出点A1、B1、C1的坐标.
四边形ABCD各顶点的坐标分别为A(1,3)、B(5,2)、C(8,4)、D(6,9),
以原点为位似中心,相似比为 的位似图形A1B1C1D1,且四边形A1B1C1D1在第一象限。
的位似图形A1B1C1D1,且四边形A1B1C1D1在第一象限。
写出各点坐标。
如图,已知△ABC的三个顶点坐标为A(0, )、B(3,
)、B(3, )、C(2,1).
)、C(2,1). 
(1)在网格图中,画出△ABC以点B为位似中心,放大到2倍后的位似△ ;
;
(2)写出 、
、 的坐标(其中
的坐标(其中 与A 对应、
与A 对应、 与C 对应)
与C 对应)
直线AB: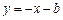 分别与x、y轴交于A
分别与x、y轴交于A 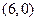 、B两点,过点B的直线交x轴负半轴于C,且
、B两点,过点B的直线交x轴负半轴于C,且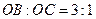 ;
;
(1)求直线BC的解析式;
(2)直线EF: (
(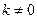 )交AB于E,交BC于点F,交x轴于D,是否存在这样的直线EF,使得
)交AB于E,交BC于点F,交x轴于D,是否存在这样的直线EF,使得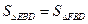 ?若存在,求出
?若存在,求出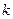 的值;若不存在,说明理由?
的值;若不存在,说明理由?
(3)P为A点右侧x轴上的一动点,以P为直角顶点、BP为腰在第一象限内作等腰直角三角形△BPQ,连结QA并延长交y轴于点K。当P点运动时,K点的位置是否发生变化?如果不变请求出它的坐标;如果变化,请说明理由。
如图:已知直线L的解析式为y=-3x+3,且L与x轴交于点D,直线m经过点A、B,直线L、m交于点C。
(1)、求直线m的解析式;
(2)、在直线m上存在异于点C的点P,使得△ADP与△ADC的面积相等,请求出点C的坐标