如图,将 的斜边 绕点 顺时针旋转 得到 ,直角边 绕点 逆时针旋转 得到 ,连接 .若 , ,且 ,则 .

如图, 点的坐标为 , 点的坐标为 , 点的坐标为 , 点的坐标为 ,小明发现:线段 与线段 存在一种特殊关系,即其中一条线段绕着某点旋转一个角度可以得到另一条线段,你认为这个旋转中心的坐标是 .

如图,边长为1的正三角形 放置在边长为2的正方形内部,顶点 在正方形的一个顶点上,边 在正方形的一边上,将 绕点 顺时针旋转,当点 落在正方形的边上时,完成第1次无滑动滚动(如图 ;再将 绕点 顺时针旋转,当点 落在正方形的边上时,完成第2次无滑动滚动(如图 , ,每次旋转的角度都不大于 ,依次这样操作下去,当完成第2016次无滑动滚动时,点 经过的路径总长为 .
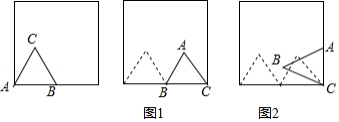
如图,在 中, , , .将 绕点 按逆时针方向旋转 得到△ ,连接 ,则△ 的面积为 .

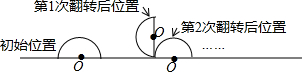
小明将量角器在桌面上进行连续翻转,如图为第1次、第2次翻转,若量角器的半径为1,则第2016次翻转后圆心 所走过的路径长为 .
如图,在矩形 中, , ,将矩形 绕点 按顺时针方向旋转得到矩形 ,点 落在矩形 的边 上,连接 ,则 的长是 .

如图, 为半圆内一点, 为圆心,直径 长为 , , ,将 绕圆心 逆时针旋转至△ ,点 在 上,则边 扫过区域(图中阴影部分)的面积为 .(结果保留

如图,在 中, , , ,将 绕点 顺时针旋转得到 (其中点 恰好落在 延长线上点 处,点 落在点 处),连接 ,则四边形 的面积为 .

如图, 是等边三角形,点 为 边上一点, ,以点 为顶点作正方形 ,且 ,连接 , .若将正方形 绕点 旋转一周,当 取最小值时, 的长为 .
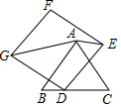
如图, 中, , ,将 绕点 顺时针旋转得到△ ,点 的对应点 落在边 上.已知 , ,则 的长为 .
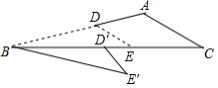
如图,在矩形 中,将 绕点 按逆时针方向旋转一定角度后, 的对应边 交 边于点 .连接 、 .若 , , ,则 (结果保留根号).
