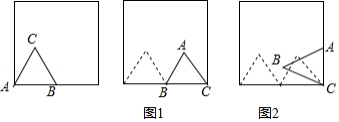
如图,边长为1的正三角形 放置在边长为2的正方形内部,顶点 在正方形的一个顶点上,边 在正方形的一边上,将 绕点 顺时针旋转,当点 落在正方形的边上时,完成第1次无滑动滚动(如图 ;再将 绕点 顺时针旋转,当点 落在正方形的边上时,完成第2次无滑动滚动(如图 , ,每次旋转的角度都不大于 ,依次这样操作下去,当完成第2016次无滑动滚动时,点 经过的路径总长为 .
如图,在边长为6的正方形内作
,
交
于点
,
交
于点
,连接
,将
绕点
顺时针旋转
得到
.若
,则
的长为 .

问题背景:如图1,将绕点
逆时针旋转
得到
,
与
交于点
,可推出结论:
.
问题解决:如图2,在中,
,
,
.点
是
内一点,则点
到
三个顶点的距离和的最小值是 .

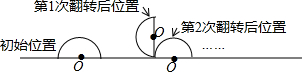
小明将量角器在桌面上进行连续翻转,如图为第1次、第2次翻转,若量角器的半径为1,则第2016次翻转后圆心 所走过的路径长为 .
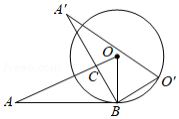
如图,为半圆的直径,且
,将半圆绕点
顺时针旋转
,点
旋转到点
的位置,则图中阴影部分的面积为 .

如图, 中, , ,将 绕点 按顺时针方向旋转 ,点 对应点 落在 的延长线上.若 ,则 .

在如图所示的方格纸格长为1个单位长度)中,
的顶点都在格点上,将
绕点
按顺时针方向旋转得到△
,使各顶点仍在格点上,则其旋转角的度数是 .

如图,在正方形网格中,格点绕某点顺时针旋转角
得到格点△
,点
与点
,点
与点
,点
与点
是对应点,则
度.

如图,在矩形 中, , ,将矩形 绕点 按顺时针方向旋转得到矩形 ,点 落在矩形 的边 上,连接 ,则 的长是 .

如图, 与 的边 相切,切点为 .将 绕点 按顺时针方向旋转得到△ ,使点 落在 上,边 交线段 于点 .若 ,则
度.
如图,将 绕点 顺时针旋转 得到△ ,已知 , ,则线段 扫过的图形(阴影部分)的面积为 .

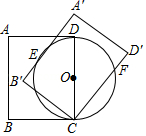
如图,在矩形 中, , ,以 为直径作 .将矩形 绕点
旋转,使所得矩形 的边 与 相切,切点为 ,边 与 相交于点
,则 的长为 .
如图,边长为4的正六边形 的中心与坐标原点 重合, 轴,将正六边形 绕原点 顺时针旋转 次,每次旋转 .当 时,顶点 的坐标为 .
