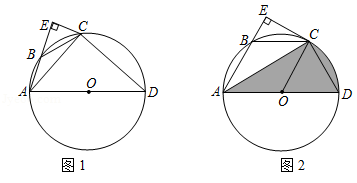
如图1,四边形 内接于 , 为直径,点 作 于点 ,连接 .
(1)求证: ;
(2)若 是 的切线, ,连接 ,如图2.
①请判断四边形 的形状,并说明理由;
②当 时,求 , 与 围成阴影部分的面积.
等面积法是一种常用的、重要的数学解题方法.它是利用“同一个图形的面积相等”、“分割图形后各部分的面积之和等于原图形的面积”、“同底等高或等底同高的两个三角形面积相等”等性质解决有关数学问题,在解题中,灵活运用等面积法解决相关问题,可以使解题思路清晰,解题过程简便快捷.
(1)在直角三角形中,两直角边长分别为3和4,则该直角三角形斜边上的高的长为 ,其内切圆的半径长为 ;
(2)①如图1, 是边长为 的正 内任意一点,点 为 的中心,设点 到 各边距离分别为 , , ,连接 , , ,由等面积法,易知 ,可得 ;(结果用含 的式子表示)

②如图2, 是边长为 的正五边形 内任意一点,设点 到五边形 各边距离分别为 , , , , ,参照①的探索过程,试用含 的式子表示 的值.(参考数据: ,
(3)①如图3,已知 的半径为2,点 为 外一点, , 切 于点 ,弦 ,连接 ,则图中阴影部分的面积为 ;(结果保留
②如图4,现有六边形花坛 ,由于修路等原因需将花坛进行改造,若要将花坛形状改造成五边形 ,其中点 在 的延长线上,且要保证改造前后花坛的面积不变,试确定点 的位置,并说明理由.

如图, 、 是 的切线, 、 是切点, 是 的直径,连接 ,交 于点 ,交 于点 .
(1)求证: ;
(2)若 恰好是 的中点,且四边形 的面积是 ,求阴影部分的面积;
(3)若 ,且 ,求切线 的长.

如图,在 中, 为 的直径, 为 的弦,点 是 的中点,过点 作 的垂线,交 于点 ,交 于点 ,分别连接 , .
(1) 与 的数量关系是 ;
(2)求证: ;
(3)若 , ,求阴影部分图形的面积.

已知平面图形 ,点 、 是 上任意两点,我们把线段 的长度的最大值称为平面图形 的“宽距”.例如,正方形的宽距等于它的对角线的长度.
(1)写出下列图形的宽距:
①半径为1的圆: ;
②如图1,上方是半径为1的半圆,下方是正方形的三条边的“窗户形“: ;
(2)如图2,在平面直角坐标系中,已知点 、 , 是坐标平面内的点,连接 、 、 所形成的图形为 ,记 的宽距为 .
①若 ,用直尺和圆规画出点 所在的区域并求它的面积(所在区域用阴影表示);
②若点 在 上运动, 的半径为1,圆心 在过点 且与 轴垂直的直线上.对于 上任意点 ,都有 ,直接写出圆心 的横坐标 的取值范围.
