如图,∠MON=60°,作边长为1的正六边形A1B1C1D1E1F1,边A1B1、F1E1分别在射线OM、ON上,边C1D1所在的直线分别交OM、ON于点A2、F2,以A2F2为边作正六边形A2B2C2D2E2F2,边C2D2所在的直线分别交OM、ON于点A3、F3,再以A3F3为边作正六边形A3B3C3D3E3F3,…,依此规律,经第n次作图后,点Bn到ON的距离是 .

下列说法正确的是
① 的值大于 ;
②正六边形的内角和是 ,它的边长等于半径;
③从一副扑克牌中随机抽取一张,它是黑桃的概率是 ;
④甲、乙两人各进行了10次射击测试,他们的平均成绩相同,方差分别是 , ,则乙的射击成绩比甲稳定.
| A. |
①②③④ |
B. |
①②④ |
C. |
①④ |
D. |
②③ |
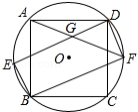
正方形 内接于 ,如图所示,在劣弧 上取一点 ,连接 、 ,过点 作 交 于点 ,连接 、 ,且 与 相交于点 ,求证:
(1)四边形 是矩形;
(2) .
据《汉书律历志》记载:“量者,龠yuè
、合、升、斗、斛
hú
也”斛是中国古代的一种量器,“斛底,方而圜
huán
其外,旁有庣
tiāo
焉”.意思是说:“斛的底面为:正方形外接一个圆,此圆外是一个同心圆”,如图所示.
问题:现有一斛,其底面的外圆直径为两尺五寸(即2.5尺),“庣旁”为两寸五分(即两同心圆的外圆与内圆的半径之差为0.25尺),则此斛底面的正方形的周长为 尺.(结果用最简根式表示)

设边长为 的等边三角形的高、内切圆的半径、外接圆的半径分别为 、 、 ,则下列结论不正确的是

| A. |
|
B. |
|
C. |
|
D. |
|
观察下列结论:
(1)如图①,在正三角形中,点
,
是
,
上的点,且
,则
,
;
(2)如图2,在正方形中,点
,
是
,
上的点,且
,则
,
;
(3)如图③,在正五边形中点
,
是
,
上的点,且
,则
,
;
根据以上规律,在正边形
中,对相邻的三边实施同样的操作过程,即点
,
是
,
上的点,且
,
与
相交于
.也会有类似的结论,你的结论是 .

阅读下列材料:
已知:如图1,等边△ 内接于 ,点 是 上的任意一点,连接 , , ,可证: ,从而得到: 是定值.

(1)以下是小红的一种证明方法,请在方框内将证明过程补充完整;
证明:如图1,作 , 交 的延长线于点 .
△ 是等边三角形,
,
又 , ,
△ △

.
,是定值.
(2)延伸:如图2,把(1)中条件“等边△ ”改为“正方形 ”,其余条件不变,请问: 还是定值吗?为什么?
(3)拓展:如图3,把(1)中条件“等边△ ”改为“正五边形 ”,其余条件不变,则 (只写出结果).
如图,正方形的边长为4,剪去四个角后成为一个正八边形,则可求出此正八边形的外接圆直径 ,根据我国魏晋时期数学家刘徽的"割圆术"思想,如果用此正八边形的周长近似代替其外接圆周长,便可估计 的值,下面 及 的值都正确的是

| A. |
, |
| B. |
, |
| C. |
, |
| D. |
, |
刘徽是中国古代卓越的数学家之一,他在《九章算术》中提出了“割圆术”,即用内接或外切正多边形逐步逼近圆来近似计算圆的面积,设圆 的半径为1,若用圆 的外切正六边形的面积 来近似估计圆 的面积,则 .(结果保留根号)
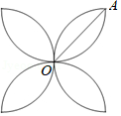
如图,用等分圆的方法,在半径为 的圆中,画出了如图所示的四叶幸运草,若 ,则四叶幸运草的周长是 .