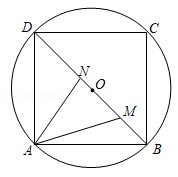
如图,正方形 内接于 ,线段 在对角线 上运动,若 的面积为 , ,则 周长的最小值是
| A. |
3 |
B. |
4 |
C. |
5 |
D. |
6 |
等面积法是一种常用的、重要的数学解题方法.它是利用“同一个图形的面积相等”、“分割图形后各部分的面积之和等于原图形的面积”、“同底等高或等底同高的两个三角形面积相等”等性质解决有关数学问题,在解题中,灵活运用等面积法解决相关问题,可以使解题思路清晰,解题过程简便快捷.
(1)在直角三角形中,两直角边长分别为3和4,则该直角三角形斜边上的高的长为 ,其内切圆的半径长为 ;
(2)①如图1, 是边长为 的正 内任意一点,点 为 的中心,设点 到 各边距离分别为 , , ,连接 , , ,由等面积法,易知 ,可得 ;(结果用含 的式子表示)

②如图2, 是边长为 的正五边形 内任意一点,设点 到五边形 各边距离分别为 , , , , ,参照①的探索过程,试用含 的式子表示 的值.(参考数据: ,
(3)①如图3,已知 的半径为2,点 为 外一点, , 切 于点 ,弦 ,连接 ,则图中阴影部分的面积为 ;(结果保留
②如图4,现有六边形花坛 ,由于修路等原因需将花坛进行改造,若要将花坛形状改造成五边形 ,其中点 在 的延长线上,且要保证改造前后花坛的面积不变,试确定点 的位置,并说明理由.

如图,圆内接正六边形的边长为4,以其各边为直径作半圆,则图中阴影部分的面积为

A. B. C. D.
小明发现相机快门打开过程中,光圈大小变化如图1所示,于是他绘制了如图2所示的图形.图2中六个形状大小都相同的四边形围成一个圆的内接正六边形和一个小正六边形,若 所在的直线经过点 , ,小正六边形的面积为 ,则该圆的半径为 .

如图,正六边形 的边长为6,以顶点 为圆心, 的长为半径画圆,则图中阴影部分的面积为

| A. |
|
B. |
|
C. |
|
D. |
|
如图,边长为 的正六边形螺帽,中心为点 , 垂直平分边 ,垂足为 , ,用扳手拧动螺帽旋转 ,则点 在该过程中所经过的路径长为 .

尺规作图特有的魅力曾使无数人沉湎其中.传说拿破仑通过下列尺规作图考他的大臣:
①将半径为 的 六等分,依次得到 , , , , , 六个分点;
②分别以点 , 为圆心, 长为半径画弧, 是两弧的一个交点;
③连接 .
问: 的长是多少?
大臣给出的正确答案应是

A. B. C. D.
如图,有一个边长不定的正方形 ,它的两个相对的顶点 , 分别在边长为1的正六边形一组平行的对边上,另外两个顶点 , 在正六边形内部(包括边界),则正方形边长 的取值范围是 .

如图,正方形的边长为4,剪去四个角后成为一个正八边形,则可求出此正八边形的外接圆直径 ,根据我国魏晋时期数学家刘徽的"割圆术"思想,如果用此正八边形的周长近似代替其外接圆周长,便可估计 的值,下面 及 的值都正确的是

| A. |
, |
| B. |
, |
| C. |
, |
| D. |
, |