阅读下列材料:
已知:如图1,等边△
内接于
,点
是
上的任意一点,连接
,
,
,可证:
,从而得到:
是定值.
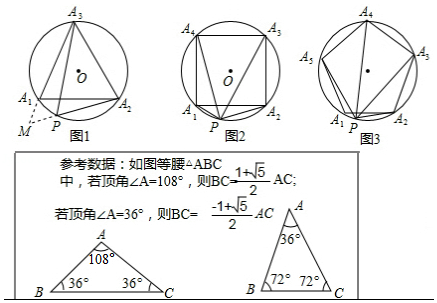
(1)以下是小红的一种证明方法,请在方框内将证明过程补充完整;
证明:如图1,作
,
交
的延长线于点
.
△
是等边三角形,
,
又
,
,
△
△

.
,是定值.
(2)延伸:如图2,把(1)中条件“等边△
”改为“正方形
”,其余条件不变,请问:
还是定值吗?为什么?
(3)拓展:如图3,把(1)中条件“等边△
”改为“正五边形
”,其余条件不变,则
(只写出结果).




 轴向右平移5个单位得到△A1B1C1,请你画出△A1B1C1
轴向右平移5个单位得到△A1B1C1,请你画出△A1B1C1 ,
, 是一元二次方程
是一元二次方程 的两根,不解方程,求
的两根,不解方程,求 +
+ 的值。
的值。 BC=6,求
BC=6,求 及b、c。
及b、c。
 粤公网安备 44130202000953号
粤公网安备 44130202000953号