如图16,在直角梯形ABCD中,AD∥BC, ,AD = 6,BC = 8,
,AD = 6,BC = 8, ,点M是BC的中点.点P从点M出发沿MB以每秒1个单位长的速度向点B匀速运动,到达点B后立刻以原速度沿BM返回;点Q从点M出发以每秒1个单位长的速度在射线MC上匀速运动.在点P,Q的运动过程中,以PQ为边作等边三角形EPQ,使它与梯形ABCD在射线BC的同侧.点P,Q同时出发,当点P返回到点M时停止运动,点Q也随之停止.
,点M是BC的中点.点P从点M出发沿MB以每秒1个单位长的速度向点B匀速运动,到达点B后立刻以原速度沿BM返回;点Q从点M出发以每秒1个单位长的速度在射线MC上匀速运动.在点P,Q的运动过程中,以PQ为边作等边三角形EPQ,使它与梯形ABCD在射线BC的同侧.点P,Q同时出发,当点P返回到点M时停止运动,点Q也随之停止.
设点P,Q运动的时间是t秒(t>0).
(1)设PQ的长为y,在点P从点M向点B运动的过程中,写出y与t之间的函数关系式(不必写t的取值范围).
(2)当BP = 1时,求△EPQ与梯形ABCD重叠部分的面积.
(3)随着时间t的变化,线段AD会有一部分被△EPQ覆盖,被覆盖线段的长度在某个时刻会达到最大值,请回答:该最大值能否持续一个时段?若能,直接写出t的取值范围;若不能,请说明理由.
某研究性学习小组在探究矩形的折纸问题时,将一块直角三角板的直角顶点绕矩形ABCD(AB<BC)的对角线的交点O旋转(①→②→③),图中的M、N分别为直角三角形的直角边与矩形ABCD的边CD、BC的交点。该学习小组成员意外的发现图①(三角板一直角边与OD重合)中,BN2=CD2+CN2,在图③中(三角板一边与OC重合),CN2=BN2+CD2,请你对这名成员在图①和图③中发现的结论选择其一说明理由。
试探究图②中BN、CN、CM、DN这四条线段之间的数量关系,写出你的结论,并说明理由。

将矩形ABCD改为边长为1的正方形ABCD,直角三角板的直角顶点绕O点旋转到图④,两直角边与AB、BC分别交于M、N,直接写出BN、CN、CM、DM这四条线段之 间所满足的数量关系(不需要证明)

在平面直角坐标系中,四边形OBCD是正方形,且D(0,2),点E是线段OB延长线上一点,M是线段OB上一动点(不包括点O、B),作MN⊥DM,垂足为M,交∠CBE的平分线于点N .写出点C的坐标;
求证:MD = MN;
连接DN交BC于点F,连接FM,下列两个结论:①FM的长度不变;②MN平分∠FMB,其中只有一个结论是正确的,请你指出正确的结论,并给出证明.

如图①所示,已知 、
、 为直线
为直线 上两点,点
上两点,点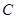 为直线
为直线 上方一动点,连接
上方一动点,连接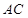 、
、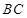 ,分别以
,分别以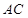 、
、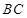 为边向
为边向 外作正方形
外作正方形 和正方形
和正方形 ,过点
,过点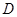 作
作 于点
于点 ,过点
,过点 作
作 于点
于点 .
.如图②,当点
 恰好在直线
恰好在直线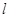 上时(此时
上时(此时 与
与 重合),试说明
重合),试说明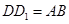 ;
;在图①中,当
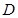 、
、 两点都在直线
两点都在直线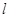 的上方时,试探求三条线段
的上方时,试探求三条线段 、
、 、
、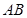 之间的数量关系,并说明理由;
之间的数量关系,并说明理由;如图③,当点
 在直线
在直线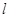 的下方时,请直接写出三条线段
的下方时,请直接写出三条线段 、
、 、
、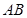 之间的数量关系.(不需要证明)
之间的数量关系.(不需要证明)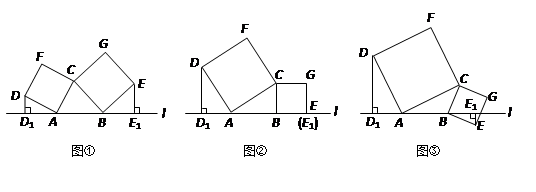
如图,在直角坐标系xoy中,O是坐标原点,点A在x正半轴上,OA= cm,点B在y轴的正半轴上,OB=12cm,动点P从点A开始沿AO以
cm,点B在y轴的正半轴上,OB=12cm,动点P从点A开始沿AO以 cm/s的速度向点O移动,移动时间为t s(0<t<6).
cm/s的速度向点O移动,移动时间为t s(0<t<6).
(1)求∠OAB的度数. (2分)
(2)以OB为直径的⊙O‘与AB交于点M,当t为何值时, PM与⊙O‘相切?
(3分)(3)动点Q从点A开始沿AB以4cm/s的速度向点B移动,动点R从点B开始沿BO以2cm/s的速度向点O移动. 如果P、Q、R分别从A、A、B同时移动,当t="4" s时,试说明四边形BRPQ为菱形;(3分)
(4)在(3)的条件下,以R为圆心,r为半径作⊙R,当r不断变化时,⊙R与菱形BRPQ各边的交点个数将发生变化,随当交点个数发生变化时,请直接写出r的对应值或取值范围.(4分)
右图中,ABCD是梯形,面积是1。已知 =
=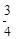 ,
,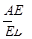 =
= ,
, =
=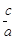 。问:
。问:

(1) 三角形ECD的面积是多少?
(2) 四边形EHFG的面积是多少?
如图,设ABCD是正方形,P是CD边的中点,点Q在BC边上,
且ÐAPQ=90°,AQ与BP相交于点T,则 的值为多少?
的值为多少?
在下列图形中,各有一边长为4cm的正方形与一个8cm×2cm的长方形相重叠.问哪一个重叠的面积最大 ( )
如右图所示,ABCD是一个正方形,其中几块阴影部分的面积如图所示,则四边形BMQN的面积为 。
如右图,在10´10的方格中有一个四边形,4个顶点在方格的格点上。 如果每个方格的面积为1,则四边形的面积是 。
下列四个命题:
①一组对边相等且一组对角相等的四边形是平行四边形; ②一组对边相等且一条对角线平分另一条对角线的四边形是平行四边形;③一组对角相等且这一组对角的顶点所联结的对角线被另一条对角线平分的四边形是平行四边形;
④一组对角相等且这一组对角的顶点所联结的对角线平分另一条对角线的四边形是平行四边形.
其中,正确命题的序号是 .
正方形ABCD的边长为5,E为边BC上一点,使得BE=3,P是对角线BD上的一点,使得PE+PC的值最小.则PB= .
在 中, ,分别过点 , 作 平分线的垂线,垂足分别为点 , , 的中点是 ,连接 , , .则下列结论错误的是
| A. |
|
B. |
|
C. |
|
D. |
|
如图,在锐角三角形 中, 是 边上的高,以 为直径的 交 于点 ,交 于点 ,过点 作 ,垂足为 ,交 于点 ,交 于点 ,连接 , , .
(1)求证: ;
(2)若 , , ,求 的长.
