2011年奥林匹克初中数学训练题
已知m、n是两个连续正整数,m<n,且a=mn,设x=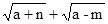 ,y=
,y= .下列说法正确的是( ).
.下列说法正确的是( ).
| A.x为奇数,y为偶数 | B.x为偶数,y为奇数 |
| C.x、y都为奇数 | D.x、y都为偶数 |
设a、b、c和S分别为三角形的三边长和面积,关于x的方程b2x2+(b2+c2-a2)x+c2=0的判别式为Δ.则Δ与S的大小关系为( ).
| A.Δ=16S2 | B.Δ=-16S2 | C.Δ=16S | D.Δ=-16S |
如图,D、E分别为△ABC的边AB、AC上的点,△ACD与△BCD的周长相等,△ABE与△CBE的周长相等,记△ABC的面积为S.若∠ACB=90°,则AD·CE与S的大小关系为( ). 
A、S=AD·CE B、S>AD·CE C、S<AD·CE D、无法确定
如图,在△ABC中,AB=8,BC=7,AC=6,延长边BC到点P,使得△PAB与△PCA相似.则PC的长是( ). 
| A.7 | B.8 | C.9 | D.10 |
如图,以PQ=2r(r∈Q)为直径的圆与一个以R(R∈Q)为半径的圆相切于点P.正方形ABCD的顶点A、B在大圆上,小圆在正方形的外部且与边CD切于点Q.若正方形的边长为有理数,则R、r的值可能是( ). 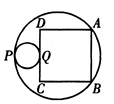
A.R=5,r="2" B.R=4,r=3/2
C.R=4,r="2" D.R=5,r=3/2
把1,2,…,2 008个正整数分成1 004组:a1,b1;a2,b2;…;a1 004,b1 004,且满足a1+b1=a2+b2=…=a1004+b1004.对于所有的i(i=1,2,…,1 004),aibi的最大值为 .
下列四个命题:
①一组对边相等且一组对角相等的四边形是平行四边形; ②一组对边相等且一条对角线平分另一条对角线的四边形是平行四边形;③一组对角相等且这一组对角的顶点所联结的对角线被另一条对角线平分的四边形是平行四边形;
④一组对角相等且这一组对角的顶点所联结的对角线平分另一条对角线的四边形是平行四边形.
其中,正确命题的序号是 .
(25分)已知G是△ABC内任一点,BG、CG分别交AC、AB于点E、F.
求使不等式S△BGF·S△CGE≤kS2△ABC恒成立的k的最小值.
 的小数部分,b为
的小数部分,b为 的小数部分.则
的小数部分.则 的值为( ).
的值为( ). +
+  -1
-1 的值为 .
的值为 .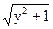 )(y+
)(y+ )=1.求证:x+y=0.
)=1.求证:x+y=0. 粤公网安备 44130202000953号
粤公网安备 44130202000953号