初中数学圆内接四边形的性质填空题

如图，正方形的边长为2，以为圆心、为半径作弧交于点，设弧与边、围成的阴影部分面积为；然后以为对角线作正方形，又以为圆心、为半径作弧交于点，设弧与边、围成的阴影部分面积为；…，按此规律继续作下去，设弧与边、围成的阴影部分面积为．则：（1）=      ；（2）=      ．

如图平行四边形ABCD中AB=AD=6，∠DAB=60度，F为AC上一点，E为AB中点，则EF+BF的最小值为        ．

如图，在正方形ABCD内作一个等边三角形ABE，连接DE、CE，有如下结论：①图中除等边三角形ABE外，还有三个等腰三角形；②△ADE≌△BCE；③此图形既是中心对称图形也是轴对称图形；④△ABE的面积与正方形ABCD的面积比是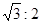；⑤△DEC与△ABE的面积比为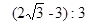。则以上结论正确的是          ．（只填正确结论的序号）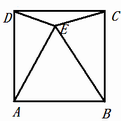

（11·天水）如图，在梯形ABCD中，AB∥CD，∠BAD＝90°，AB＝6，对角线
AC平分∠BAD，点E在AB上，且AE＝2（AE＜AD），点P是AC上的动点，则PE＋PB
的最小值是_  ▲  ．

如图，正方形ABCD的边长为2，点E是BC边的中点，过点B作BG⊥AE，
垂足为G，延长BG交AC于点F，则CF=         ．

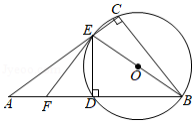
如图，在 $\text{Rt}\Delta \text{ABC}$ 中， $\angle C=90°$ ， $\mathit{AB}$ 的垂直平分线分别交 $\mathit{AB}$ 、 $\mathit{AC}$ 于点 $D$ 、 $E$ ， $\mathit{BE}=8$ ， $\odot O$ 为 $\mathit{\Delta BCE}$ 的外接圆，过点 $E$ 作 $\odot O$ 的切线 $\mathit{EF}$ 交 $\mathit{AB}$ 于点 $F$ ，则下列结论正确的是 　　 $.$ （写出所有正确结论的序号）

① $\mathit{AE}=\mathit{BC}$ ；

② $\angle \mathit{AED}=\angle \mathit{CBD}$ ；

③若 $\angle \mathit{DBE}=40°$ ，则 $\widehat{\mathit{DE}}$ 的长为 $\frac{8\pi }{9}$ ；

④ $\frac{\mathit{DF}}{\mathit{EF}}=\frac{\mathit{EF}}{\mathit{BF}}$ ；

⑤若 $\mathit{EF}=6$ ，则 $\mathit{CE}=2.24$ ．

如图，边长为1的菱形ABCD中，∠DAB=60度．连接对角线AC，以AC为边作第二个菱形ACC₁D₁，使∠D₁AC=60°；连接AC₁，再以AC₁为边作第三个菱形AC₁C₂D₂，使∠D₂AC₁=60°；…，按此规律所作的第n个菱形的边长为         ．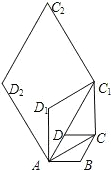

（11·贺州）把一张矩形纸片ABCD按如图方式折叠，使顶点B和顶点D重合，
折痕为EF．若BF＝4，FC＝2，则∠DEF的度数是_   ▲   ．

（11·佛山）在矩形ABCD中，两条对角线AC、BD相交于点O，若AB＝OB＝4，则AD＝ ；

如图，在□ABCD中，AC、BD相交于点O，点E是AB的中点．若OE＝3cm，则AD的长是       cm．

在Rt△ABC中，∠C=90°，AC=3，BC=4，将△ABC绕边AC所在直线旋转一周得到圆锥，则该圆锥的侧面积是___________.

如图，D，E，F分别为△ABC三边的中点，则图中平行四边形的个数为　．

如图，在正方形ABCD中，边长为2的等边三角形AEF的顶点E、F分别在BC和CD上，下列结论：
①CE=CF；②∠AEB=75°；③BE+DF=EF；④S_{正方形ABCD}=2+
其中正确的序号是______________

如图,在□ABCD中，AB=3，AD=4，∠ABC=60°，过BC的中点E作EF⊥AB，垂足为点F，与DC的延长线相交于点H，则△DEF的面积是 ▲ .

如图6，已知菱形ABCD，其顶点A、B在数轴上对应的数分别为－4和1，则
BC=_____.