如图,△ABC中,AD是边BC上的中线,过点A作AE∥BC,过点D作DE∥AB与AC、AE分别交于点O、点E,连接EC.
(1)求证:AD=EC;
(2)当∠BAC=90°时,求证:四边形ADCE是菱形;
(本题10分)(1)如图1,已知∠AOB,OA=OB,点E在OB边上,四边形AEBF 是平行四边形,请你只用无刻度的直尺在图中画出∠AOB的平分线.(保留作图痕迹,不要求写作法)
(2)如图2,在10×10的正方形网格中,点A(0,0)、B(5,0)、C(3,6)、D(-1,3),
①依次连结A、B、C、D四点得到四边形ABCD,四边形ABCD的形状是 ▲ .
②在x轴上找一点P,使得△PCD的周长最短(直接画出图形,不要求写作法);
此时,点P的坐标为 ▲ ,最短周长为 ▲ .
(本题6分)已知:如图,在等腰梯形ABCD中,AB//CD,点E、分别在AD、BC上,且DE=CF.求证:AF=BE

如图,四边形ABCD为直角梯形 ,AD‖BC,
,AD‖BC, ,
, ,
, .
. 动点P、Q分别从A、C两点同时出发,点P以每秒1个单
动点P、Q分别从A、C两点同时出发,点P以每秒1个单
位的速度由A向D运动,点Q以每秒2个单位的速度由C向B运动,当点Q停
止运动时,点P也停止运动,设运动时间为 (0≤
(0≤ ≤5),
≤5),
(1)当t为多少时,四边形PQCD是平行四边形?
(2)当t为多少时,四边形PQCD是等腰梯形?
如图,在□  中,E,F分别为边AB,CD的中点,连接DE,BF,BD.
中,E,F分别为边AB,CD的中点,连接DE,BF,BD.
(1)求证:△ADE≌△CBF.
(2)若AD⊥BD,则四边形BFDE是什么特殊四边形?请证明你的结论.
如图,点E是正方形ABCD的边DC上一点,把△ADE顺时针旋转△ABF的位置.(1)旋转中心是点 ,旋转角度是
 度;
度;(2)若连结EF,则△AEF是 三角形;
(3)若四边形AECF的面积为25,DE=2,求AE的长.

已知:如图,梯形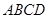 中,
中,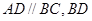 平分
平分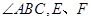 分别为AD、AB中点,点G为BC边上一点,且
分别为AD、AB中点,点G为BC边上一点,且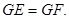
(1)求证:
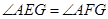 ;
;(2)猜想:当
 时,四边形
时,四边形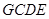 为平行
为平行 四边形,并说明理由.
四边形,并说明理由.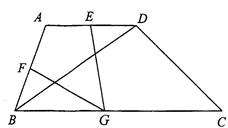
.(本题8分)如图,在正方形ABCD中,E为对角线AC上一点,连接EB、ED.
(1) 写出图中所有的全等三角形
(2) 延长BE交AD于点F,若∠DEB = 140°,求∠AFE的度数.
如图,梯形ABCD中,AD∥BC,AB = BC = DC,点E、F分别在AD、AB上,且 .
.
(1)求证:
 ;
;(2)连结AC,若
 ,求
,求 的度数.
的度数.
如图,在平行四边形ABCD中,E、F分别为边AB、CD的中点,BD是对角线,过A点作AG∥DB交CB的延长线于点G.
(1)求证:DE∥BF;
(2)若∠G=90
 ,求证四边形DEBF是菱形.
,求证四边形DEBF是菱形.
.已知:如图,□ABCD中,对角线AC,BD相交于点O,延长CD至F,使DF=CD,连接BF交AD于点E.
(1)求证:AE=ED;
(2)若AB=BC,求∠CAF的度数.
图形的操作过程如下(本题中四个矩形的水平方向的边长均为a,竖直方向的边长均为b)在图①中,将线段A1A2向右平移1个单位长度到B1B2,得到封闭图形A1A2B2B1(即阴影部分);在图②中,将折线A1A2A3(其中A2叫做折线A1A2A3的一个“折点”)向右平移1个单位长度到B1B2B3,得到封闭图形A1A2A2B3B2B1(即阴影部分)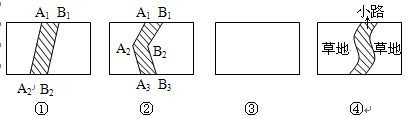
(1)在图③中,请你类似地画一条有两个折点的折线,同样向右平移1个单位长度,从而得到一个封闭图形,并用斜线画出阴影部分.
(2)分别求出①,②,③三个图形中除去阴影部分后剩余部分的面积.
(3)联想与探索:如图④所示,在一块矩形草地上,有一条弯曲的柏油小路(小路的水平宽度是1个单位长度),请你猜想空白部分的草地面积是多少?并说明你的猜想是正确的.
如图所示,已知△ABC是等边三角形,点D、F分别在线段BC,AB上,∠EFB=60º,DC=EF.

(1)求证:四边形EFCD是平行四边形;
(2)若BF=EF,求证AE=AD
如图, ABCD的对角线AC的垂直平分线EF与边AD,BC分别交于E、F点
求证:四边形AFCE是菱形
如右图,直线d过正方形ABCD的顶点B,点A,C到直线d的距离分别是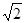 和2
和2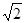 ,求正方形ABCD的对角线AC的长.
,求正方形ABCD的对角线AC的长.