[北京]2010–2011学年北京市西城区八年级第二学期抽样测试数学卷
下列各组数中,以它们为边长的线段不能构成直角三角形的是( ).
| A.6,8,10 | B.8,15,17 | C.1, ,2 ,2 |
D.2,2, |
对角线相等且互相平分的四边形一定是( )
| A.等腰梯形 | B.矩形 | C.菱形 | D.平行四边形 |
如图,等腰梯形ABCD中,AD∥BC,BD平分∠ABC,∠DBC=30°,AD=5,则BC等于( ).
| A.5 | B.7.5 | C. |
D.10 |
右图为在某居民小区中随机调查的10户家庭一年的月均用水量(单位:t)的条形统计图,则这10户家庭月均用水量的众数和中位数分别是( ).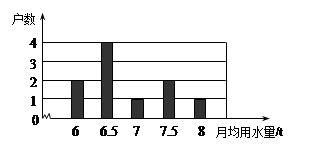
| A.6.5,7 | B.6.5,6.5 |
| C.7,7 | D.7,6.5 |
如图,反比例函数 (
( )的图象与一次函数
)的图象与一次函数 的图象交于点
的图象交于点 和点
和点 ,当
,当 时,
时, 的取值范围是( ).
的取值范围是( ).
A. |
B. 或 或 |
C. |
D. 或 或 |
如图,正方形ABCD中,AB=4,点E,F分别在AD,DC上,且△BEF为等边三角形,则△EDF与△BFC的面积比为( ).
| A.2:1 | B.3:1 | C.3:2 | D.5:3 |
在“2011年北京郁金香文化节”中,北京国际鲜花港的 株郁金香为京城增添了亮丽的色彩.若这些郁金香平均每平方米种植的数量为
株郁金香为京城增添了亮丽的色彩.若这些郁金香平均每平方米种植的数量为 (单位:株/平方米),总种植面积为
(单位:株/平方米),总种植面积为 (单位:平方米),则
(单位:平方米),则 与
与 的函数关系式为____________________.(不要求写出自变量
的函数关系式为____________________.(不要求写出自变量 的取值范围)
的取值范围)
如图,矩形ABCD中,对角线AC,BD交于点O,∠AOD=120°,BD=8,则AB的长为___________.
菱形ABCD中,AB=2,∠ABC=60°,顺次连接菱形ABCD各边的中点所得四边形的面积为____________.
如图,□ABCD中,点E在AB边上,将△EBC沿CE所在直线折叠,使点B落在AD边上的点B′处,再将折叠后的图形打开,若△AB′E的周长为4cm,△B′DC的周长为11cm,则B′D的长为_________cm.
正方形网格中,每个小正方形的边长为1.图1所示的矩形是由4个全等的直角梯形拼接而成的(图形的各顶点都在格点上;拼接时图形互不重叠,不留空隙),如果用这4个直角梯形拼接成一个等腰梯形,那么(1)仿照图1,在图2中画出一个拼接成的等腰梯形;(2)这个拼接成的等腰梯形的周长为________.
如图,在平面直角坐标系 中,
中, ,
, ,
, ,
, ,……,以
,……,以 为对角线作第一个正方形
为对角线作第一个正方形 ,以
,以 为对角线作第二个正方形
为对角线作第二个正方形 ,以
,以 为对角线作第三个正方形
为对角线作第三个正方形 ,……,顶点
,……,顶点 ,
, ,
, ,……都在第一象
,……都在第一象 限,按照这样的规律依次进行下去,点
限,按照这样的规律依次进行下去,点 的坐标为__________;点
的坐标为__________;点 的坐标为_________________.
的坐标为_________________.
.已知:如图,□ABCD中,对角线AC,BD相交于点O,延长CD至F,使DF=CD,连接BF交AD于点E.
(1)求证:AE=ED;
(2)若AB=BC,求∠CAF的度数.
甲,乙两人是NBA联盟凯尔特人队的两位明星球员,两人在前五个赛季的罚球
命中率如下表所示:
| 甲球员的命中率(%) |
87 |
86 |
83 |
85 |
79 |
| 乙球员的命中率(%) |
87 |
85 |
84 |
80 |
84 |
(1)分别求出甲,乙两位球员在前五个赛季罚球的平均命中率;
(2)在某场比赛中,因对方球员技术犯规需要凯尔特人队选派一名队员进行罚球,你认为甲,乙两位球员谁来罚球更好?(请通过计算说明理由)
为了增强员工的团队意识,某公司决定组织员工开展拓展活动.从公司到拓展活动地点的路程总长为126千米,活动的组织人员乘坐小轿车,其他员工乘坐旅游车同时从公司出发,前往拓展活动的目的地.为了在员工们到达之前做好活动的准备工作,小轿车决定改走高速公路,路程比原路线缩短了18千米,这样比按原路线行驶的旅游车提前24分钟到达目的地.已知小轿车的平均速度是旅游车的平均速度的1.2倍,求这两种车平均每小时分别行驶多少千米.
已知:如图,梯形ABCD中,AD∥BC,∠B=90°,AD= ,BC=
,BC= ,DC=
,DC= ,
,
且 ,点M是AB边的中点.
,点M是AB边的中点.
(1)求证:CM⊥DM;
(2)求点M到CD边的距离.(用含
 ,
, 的式子表示)
的式子表示)
已知:如图1,直线 与双曲线
与双曲线 交于A,B两点,且点A的坐标为(
交于A,B两点,且点A的坐标为( ).
).
(1)求双曲线
 的解析式;
的解析式;(2)点C(
 )在双曲线
)在双曲线 上,求△AOC的面积;
上,求△AOC的面积;(3)过原点O作另一条直线
 与双曲线
与双曲线 交于P,Q两点,且点P在第一象限.若由点A,P,B,Q为顶点组成的四边形的面积为20,请直接写出所有符合条件的点P的坐标.
交于P,Q两点,且点P在第一象限.若由点A,P,B,Q为顶点组成的四边形的面积为20,请直接写出所有符合条件的点P的坐标.
已知:如图1,平面直角坐标系 中,四边形OABC是矩形,点A,C的坐标分别为(6,0),(0,2).点D是线段BC上的一个动点(点D与点B,C不重合),过点D作直线
中,四边形OABC是矩形,点A,C的坐标分别为(6,0),(0,2).点D是线段BC上的一个动点(点D与点B,C不重合),过点D作直线 =-
=- +
+ 交折线O-A-B于点E.
交折线O-A-B于点E.
(1)在点D运动的过程中,若△ODE的面积为S,求S与
 的函数关系式,
的函数关系式, 并写出自变量的取值范围;
并写出自变量的取值范围;(2)如图2,当点E在线段OA上时,矩形OABC关于直线DE对称的图形为矩形O′A′B′C′,C′B′分别交CB,OA于点D,M,O′A′分别交CB,OA于点N,E.探究四边形DMEN各边之间的数量关系,并对你的结论加以证明;

(3)问题(2)
 中的四边形DMEN中,ME的长为____________.
中的四边形DMEN中,ME的长为____________.
问题1 已知:如图1,三角形ABC中,点D是AB边的中点,AE⊥BC,BF⊥AC,垂足分别为点E,F,AE,BF交于点M,连接DE,DF.若DE=
 DF,则
DF,则 的值为____
的值为____ _.
_. 
拓展
问题2 已知:如图2,三角形ABC中,CB=CA,点D是AB边的中点,点M在三角形ABC的内部,且∠MAC=∠MBC,过点M分别作ME⊥BC,MF⊥AC,垂足分别为点E,F,连接DE,DF.求证:DE=DF.
推广
问题3 如图3,若将上面问题2中的条件“CB=CA”变为“CB≠CA”,其他条件不变,试探究DE与DF之间的数量关系,并证 明你的结论.
明你的结论.
 中,自变量
中,自变量 的取值范围是( ).
的取值范围是( ).
 >0时,
>0时, 随
随



 的方程
的方程 有两个不相等的实数根,则
有两个不相等的实数根,则 的取值范围是( ).
的取值范围是( ).



 ,下列变形正确的是( ).
,下列变形正确的是( ).



 ,则
,则 的值为___________
的值为___________ ,则代数式
,则代数式 的值为__________.
的值为__________. ;
;  .
. 1)
1) ;
;  .
. 粤公网安备 44130202000953号
粤公网安备 44130202000953号