[湖北]2011-2012学年湖北省宜昌市长阳县九年级第一学期期末模拟数学卷
方程ⅹ(ⅹ-1)=0的解是(■)
| A.x=0 | B.x=1 | C.x= 0或ⅹ=1 | D.x=0和ⅹ=1 |
x1,x2是方程2x2-4x+1=0的两根,则x1 + x2=(■).
| A.2 | B.-2 | C.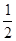 |
D.-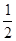 |
下列三角形中,是正三角形的为( ).
① 有一个角是60°的等腰三角形; ②有两个角是60°的三角形;
③底边与腰相等的等腰三角形; ④三边相等的三角形;
| A.①④ | B.②③ | C.③④ | D.①②③④ |
如图, 山坡AC与水平面AB成30°的角,沿山坡AC每往上爬100米,则竖直高度上升(■)米.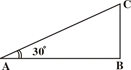
A. |
B.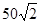 |
| C.50 | D.30 |
桌上有十个苹果,要把这十个苹果放到九个抽屉里,对于“有一个抽屉里面至少放有两个苹果”的概率为(■).
| A.1 | B.0.9 | C.0.5 | D. |
如图,在Rt△ACB中,∠C=90°,BE平分∠CBA交AC于 点E,过E作ED⊥AB于D点,当∠A=_____时, ED恰为 AB的中垂线.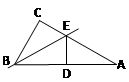
| A.10° | B.15° | C.30° | D.45° |
在平行四边形ABCD中(AB>BC),点E、F分别在AB、CD上移动,且AE=CF,则四边形BFDE的形状不可能是(■).
A. 矩形 B. 菱形
C. 平行四边形 D. 梯形
在太阳光下,小李在地面上同时摆弄两根长度不相等的竹竿,若它们的影子长度相等,则这两根竹竿的相对位置可能是(■).
| A.两根都垂直于地面 | B.两根都倒在地面上 |
| C.两根不平行斜竖在地面上 | D.两根平行斜竖在地面上 |
面积为20平方厘米的矩形,其长宽分别为ⅹ厘米和y厘米,则y与x之间的函数关系式的图象为(■).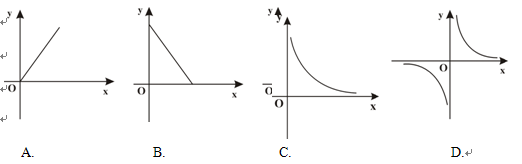
在一个暗箱中,只装有a个白色乒乓球和10个黄色乒乓球,每次搅拌均匀后,任意摸出一个球后又放回,通过大量重复摸球实验后发现,摸到黄球的频率稳定在40%,那么暗箱中的乒乓球共有■个.
如图,在直角坐标系中,A点、B点坐标分别为(2,0),(0,1),要使四边形BOAC为矩形,则C点坐标为 ■.
如图,已知E、F、G、H是四边形ABCD四边的中点,则四边形EFGH的形状为■;如四边形ABCD的对角线AC 与BD的和为40,则四边形EFGH的周长为■.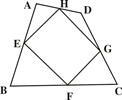
已知点A(k+1,2)在双曲线y= 上,试判断双曲线y= 与直线y=x+1有无交点.
如右图,直线d过正方形ABCD的顶点B,点A,C到直线d的距离分别是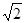 和2
和2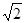 ,求正方形ABCD的对角线AC的长.
,求正方形ABCD的对角线AC的长.
如图,在高楼AB前D点测得楼顶A的仰角为30°,向高楼前进60米到达C点处,又测得仰角为45°,求高楼的高度为多少?(结果精确到0.1米, ≈1.414,
≈1.414,
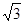 ≈1.732)
≈1.732)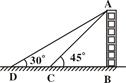
如图,在△ABC中,AB=AC.(1)请作出AB的中垂线DE,交AC于D交AB于E.(不写作法,保留作图痕迹)
(2)如果BD=BC,求∠A的度数.

小张同学将清洗后的一黑一白的两双相同型号及大小的运动袜子放在衣柜抽屉里,当他随意从抽屉里抽出两只袜子时,请你选用恰当的方式分析恰好成双的机会与不成双的机会.
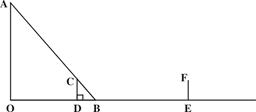
如右图,路灯A离地8米,身高1.6米的小王(C D)的影长DB与身高一样,现在他沿OD方向走10米,到达E处.(1)请画出小王在E处的影子EH;
(2)求EH的长.
如右图,在等腰梯形ABCD中,AD∥BC,AD=AB.过A作AF⊥BD,交BC于G,延长BC至E,使CE=CD.(1)请指出四边形ACED的形状,并证明;
(2)如果BD=8,AG=6,求△BDE的面积.
某化工企业每月生产收入40万元,按季度要上缴生产收入的25%作为税收,同时
在生产过程中产生的污水每月定额3万元的治污费交由污水厂处理.企业管理层决定从
2011年元月起,投资100万元自行配置治污设备,工期半年. 7月份设备上马后,就不需交纳治污费.同时治污设备使水得到了循环使用,会使三、四季度生产收入逐季上升,之后生产收入便稳定在四季度水平. 另外国家为了鼓励企业自已治污,会将每季税率由25%改为10%征收. 预计2011年四季度的毛利比一季度的毛利多38.07万元.
(毛利=生产收入-税收-治污费)(1)2011年前六个月上缴的税金预计为多少?
(2)单从节约的治污费和税收考虑,到2012年7月份前,能否抵回100万元的设备投资款.
(3)求2011年三、四季度生产收入的平均增长率.
(供参考数据:1.052="1.1025 " 1.062="1.1236 " 1.082="1.1664 " 1.12=1.21)
 粤公网安备 44130202000953号
粤公网安备 44130202000953号