如图,点O是矩形ABCD的中心,E是AB上的点,沿CE折叠后,点B恰好与点O重合,若BC=3,则折痕CE的长为( )

A. |
B.2 |
C.2 | D.3 |
如图,将正方形OABC放在平面直角坐标系中,O是原点,A的坐标为(1, ),则点C的坐标为( )
),则点C的坐标为( )

A.(-1, ) ) |
B.(- ,1) ,1) |
C.(-2,1) | D.(-1,2) |
如图,四边形 是 的内接四边形, 与 的延长线交于点 , 与 的延长线交于点 , , ,则 的度数为

A. B. C. D.
如图所示,把一个长方形纸片沿EF折叠后,点D,C分别落在D′,C′的位置.若∠EFB=65°,则∠AED′等于( )

| A.70° | B.65° | C.50° | D.25° |
一个n边形的内角和比它的外角和至少大120°,则n的最小值是( ).
| A.4 | B.5 | C.6 | D.7 |
如图,过矩形ABCD的四个顶点作对角线AC、BD的平行线,分别相交于E、F、G、H四点,则四边形EFGH为( ).

A.平行四边形 B.矩形 C.菱形 D.正方形
如图,正方形ABCD的对角线BD长为2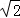 ,若直线满足:(1)点D到直线的距离为1;(2)A、C两点到直线的距离相等,则符合题意的直线的条数为( )
,若直线满足:(1)点D到直线的距离为1;(2)A、C两点到直线的距离相等,则符合题意的直线的条数为( )
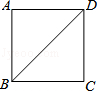
A.2 B.3 C.4 D.6
如图,在四边形ABCD中,AD∥BC,∠C=90°,BC=CD=8,过点B作EB⊥AB,交CD于点E.若DE=6,则AD的长为( )

| A.6 | B.8 | C.10 | D.无法确定 |
如图,在菱形ABCD中,AB=5,∠B=60°,则对角线AC的长等于( )

| A.8 | B.7 | C.6 | D.5 |
如图,G,E分别是正方形ABCD的边AB,BC的点,且AG=CE,AE⊥EF,AE=EF,现有如下结论:
①BE= GE;②△AGE≌△ECF;③∠FCD=45°;④△GBE∽△ECH
GE;②△AGE≌△ECF;③∠FCD=45°;④△GBE∽△ECH
其中,正确的结论有( )

| A.1个 | B.2个 | C.3个 | D.4个 |
如图,点 , 在以 为直径的半圆上,且 ,点 是 上任意一点,连接 、 .则 的度数为
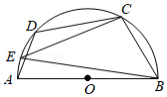
| A. |
|
B. |
|
C. |
|
D. |
|
我们已经接触了很多代数恒等式,知道可以用一些硬纸片拼成的图形面积来解释一些代数恒等式.例如图甲可以用来解释(a+b)2-(a-b)2=4ab.那么通过图乙面积的计算,验证了一个恒等式,此等式是( )

| A.a2-b2=(a+b)(a-b) |
| B.(a-b)(a+2b)=a2+ab-b2 |
| C.(a-b)2=a2-2ab+b2 |
| D.(a+b)2=a2+2ab+b2 |
已知矩形ABCD,一条直线将该矩形ABCD分割成两个多边形,若这两个多边形的内角和分别为M和N,M+N不可能是( )
| A.360° | B.540° | C.720° | D.630° |