如图,已知菱形ABCD的对角线AC、BD的长分别为6cm,8cm,AE⊥BC于点E,则AE的长是( )

A. cm B.
cm B. cm C.
cm C. cm D.
cm D. cm
cm
以不在同一直线上的三个点为顶点作平行四边形,最多能作()
| A.4个 | B.3个 | C.2个 | D.1个 |
如图,在矩形AOBC中,点A的坐标是(﹣2,1),点C的纵坐标是4,则B、C两点的坐标分别是( )

A.( ,3)、(﹣
,3)、(﹣ ,4)
,4)
B.( )、(﹣
)、(﹣ )
)
C.( )、(﹣
)、(﹣ )
)
D.( )、(﹣
)、(﹣ )
)
如图,某农场有一块四边形ABCD的空地,其各边中点分别是E、F、G、H,测得对角线AC=BD=12米,现想用篱笆围成四边形EFGH的场地,则需用的篱笆总长度是( )

| A.12米 | B.24米 | C.36米 | D.48米 |
如图,四边形ABCD中,∠ABC=3∠CBD,∠ADC=3∠CDB,∠C=130°,则∠A的度数是( )

| A.60° | B.70° | C.80° | D.90° |
如图,在平行四边形ABCD中,下列结论中错误的是( )

| A.∠1=∠2 | B.∠BAD=∠BCD | C.AB=CD | D.AC⊥BD |
下列命题是真命题的是( )
| A.四边都相等的四边形是矩形 |
| B.菱形的对角线相等 |
| C.对角线互相垂直的四边形是正方形 |
| D.对角线相等的菱形是正方形 |
下列个命题中,是真命题的是( )
| A.若x>y,则x2>y2 |
B.若(x1,y1)、(x2,y2)是函数 图象上的两点,且x1<x2,则y1>y2 图象上的两点,且x1<x2,则y1>y2 |
| C.有两角及一边对应相等的两个三角形全等 |
| D.对角线互相垂直的平行四边形是正方形 |
如图,图1、图2、图3分别表示甲、乙、丙三人由A地到B地的路线图(箭头表示行进的方向).其中E为AB的中点,AH>HB,判断三人行进路线长度的大小关系为( )
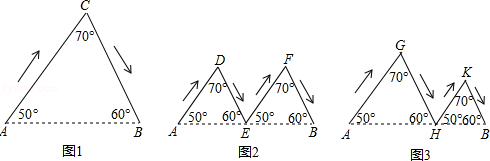
| A.甲<乙<丙 | B.乙<丙<甲 | C.丙<乙<甲 | D.甲=乙=丙 |
如图,在△ABC中,∠C=70°,沿图中虚线截去∠C,则∠1+∠2=( )

| A.140° | B.180° | C.250° | D.360° |
如图,在菱形ABCD中,AB=5,∠B=60°,则对角线AC的长等于( )

| A.8 | B.7 | C.6 | D.5 |
如图,G,E分别是正方形ABCD的边AB,BC的点,且AG=CE,AE⊥EF,AE=EF,现有如下结论:
①BE= GE;②△AGE≌△ECF;③∠FCD=45°;④△GBE∽△ECH
GE;②△AGE≌△ECF;③∠FCD=45°;④△GBE∽△ECH
其中,正确的结论有( )

| A.1个 | B.2个 | C.3个 | D.4个 |
如图,点 , 在以 为直径的半圆上,且 ,点 是 上任意一点,连接 、 .则 的度数为
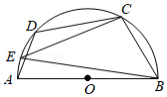
| A. |
|
B. |
|
C. |
|
D. |
|
我们已经接触了很多代数恒等式,知道可以用一些硬纸片拼成的图形面积来解释一些代数恒等式.例如图甲可以用来解释(a+b)2-(a-b)2=4ab.那么通过图乙面积的计算,验证了一个恒等式,此等式是( )

| A.a2-b2=(a+b)(a-b) |
| B.(a-b)(a+2b)=a2+ab-b2 |
| C.(a-b)2=a2-2ab+b2 |
| D.(a+b)2=a2+2ab+b2 |