有下列说法:①正方形是中心对称图形,又是轴对称图形;②矩形的对角线互相垂直;③平行四边形相邻的两个内角互补;④菱形的对角线相等.其中说法正确的个数是( )
| A.1 | B.2 | C.3 | D.4 |
如图,在正方形ABCD中,AC、BD相交于点O,把△ABC折叠,使AB落在AC上,点B与AC上的点E重合,展开后,折痕AG交BD于点F,连结EG、EF.下列结论:①tan∠AGB=2;②图中有9对全等三角形;③若将△GEF沿EF折叠,则点G不一定落在AC上;④BG=BF;⑤S四边形GFOE=S△AOF,上述结论中正确的个数是( )

A.1个 B.2个 C.3个 D.4个
如图,小聪在作线段AB的垂直平分线时,他是这样操作的:分别以A和B为圆心,大于 AB的长为半径画弧,两弧相交于C、D,则直线CD即为所求.根据他的作图方法可知四边形ADBC一定是( )
AB的长为半径画弧,两弧相交于C、D,则直线CD即为所求.根据他的作图方法可知四边形ADBC一定是( )

A.矩形 B.菱形 C.正方形 D.等腰梯形
矩形,菱形,正方形都具有的性质是( )
| A.每一条对角线平分一组对角 |
| B.对角线相等 |
| C.对角线互相平分 |
| D.对角线互相垂直 |
如图,E、F分别是正方形ABCD的边CD、AD上的点,且CE=DF,AE、BF相交于点O,下列结论:(1)AE=BF;(2)AE⊥BF;(3)AO=OE;(4)S△AOB=S四边形DEOF中正确的有( )
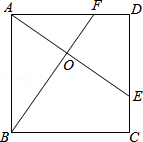
A. 4个 B.3个 C.2个 D.1个
如图,已知菱形ABCD的对角线AC、BD的长分别为6cm、8cm,AE⊥BC于点E,则AE的长是( )

A. cm B.
cm B. cm C.
cm C. cm D.
cm D. cm
cm
如图,四边形ABCD和四边形AEFC是两个矩形,点B在EF边上,若矩形ABCD和矩形AEFC的面积分别是S1、S2的大小关系是( )

| A.S1>S2 | B.S1=S2 | C.S1<S2 | D.3S1=2S2 |
下列命题是真命题的是( )
| A.四边都相等的四边形是矩形 |
| B.菱形的对角线相等 |
| C.对角线互相垂直的四边形是正方形 |
| D.对角线相等的菱形是正方形 |
如图,点O是矩形ABCD的中心,E是AB上的点,沿CE折叠后,点B恰好与点O重合,若BC=3,则折痕CE的长为( )

A. |
B.2 |
C.2 | D.3 |
如图,菱形ABCD的周长为40cm,对角线AC、BD相交于点O,DE⊥AB,垂足为E,DE:AB=4:5,则下列结论:①DE=8cm;②BE=4cm;③BD=4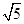 cm;④AC=8
cm;④AC=8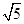 cm;⑤S菱形ABCD=80cm,正确的有( )
cm;⑤S菱形ABCD=80cm,正确的有( )
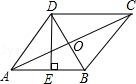
A.①②④⑤ B.①②③④ C.①③④⑤ D.①②③④⑤
矩形的两边长分别是3和5,则它的对角线长是( )
| A.4 | B.6 | C.7 | D. |
如图,在菱形ABCD中,AB=5,∠B=60°,则对角线AC的长等于( )

| A.8 | B.7 | C.6 | D.5 |
如图,G,E分别是正方形ABCD的边AB,BC的点,且AG=CE,AE⊥EF,AE=EF,现有如下结论:
①BE= GE;②△AGE≌△ECF;③∠FCD=45°;④△GBE∽△ECH
GE;②△AGE≌△ECF;③∠FCD=45°;④△GBE∽△ECH
其中,正确的结论有( )

| A.1个 | B.2个 | C.3个 | D.4个 |
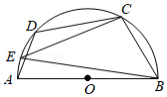
如图,点 , 在以 为直径的半圆上,且 ,点 是 上任意一点,连接 、 .则 的度数为
| A. |
|
B. |
|
C. |
|
D. |
|