如图,在菱形ABCD中,对角线AC=4,BD=9,则菱形ABCD的面积为( )

| A.12 | B.18 | C.20 | D.36 |
如图,在矩形ABCD中,AB= ,BC=3,将△ABC沿对角线AC折叠,点B恰好落在点P处,CP与AD交于点F,连接BP交AC于点G,交AD于点E,下列结论错误的是( )
,BC=3,将△ABC沿对角线AC折叠,点B恰好落在点P处,CP与AD交于点F,连接BP交AC于点G,交AD于点E,下列结论错误的是( )

| A.AC="2AP" | B.△PBC是等边三角形 |
| C.S△BGC=3S△AGP | D. = = |
如图,菱形ABCD的周长为20,一条对角线AC长为8,另一条对角线BD长为( )

| A.16 | B.12 | C.6 | D.4 |
如图,已知在矩形ABCD中,AB=4,BC=2,点M,E在AD上,点F在边AB上,并且DM=1,现将△AEF沿着直线EF折叠,使点A落在边CD上的点P处,则当PB+PM的和最小时,ME的长度为( )
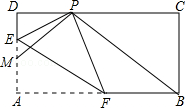
A.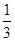 |
B.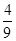 |
C.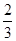 |
D.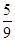 |
如图,在菱形ABCD中,AB=2,∠BAD=60°,E是AB的中点,P是对角线AC上的一个动点,则PE+PB的最小值为( )

| A.1 | B. |
C.2 | D. |
已知:如图,菱形ABCD中,对角线AC与BD相交于点O,OE∥DC交BC于点E,AD=6cm,则OE的长为( )

| A.6cm | B.4cm | C.3cm | D.2cm |
下列命题是真命题的是( )
| A.四边都相等的四边形是矩形 |
| B.菱形的对角线相等 |
| C.对角线互相垂直的四边形是正方形 |
| D.对角线相等的菱形是正方形 |
如图,四边形ABCD的对角线交于点O,下列哪组条件不能判断四边形ABCD是平行四边形( )

| A.OA=OC,OB=OD |
| B.∠BAD=∠BCD,AB∥CD |
| C.AD∥BC,AD=BC |
| D.AB=CD,AO=CO |
如图,平行四边形ABCD和矩形ACEF的位置如图所示,点D在EF上,则平行四边形ABCD和矩形ACEF的面积S1、S2的大小关系是( )

| A.S1>S2 | B.S1=S2 | C.S1<S2 | D.3S1=2S2 |
如图,下列条件中,能使▱ABCD成为菱形的是( )

| A.AB="CD" | B.AD="BC" | C.AB="BC" | D.AC=BD |
如图,在菱形ABCD中,AB=5,∠B=60°,则对角线AC的长等于( )

| A.8 | B.7 | C.6 | D.5 |
如图,G,E分别是正方形ABCD的边AB,BC的点,且AG=CE,AE⊥EF,AE=EF,现有如下结论:
①BE= GE;②△AGE≌△ECF;③∠FCD=45°;④△GBE∽△ECH
GE;②△AGE≌△ECF;③∠FCD=45°;④△GBE∽△ECH
其中,正确的结论有( )

| A.1个 | B.2个 | C.3个 | D.4个 |
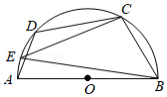
如图,点 , 在以 为直径的半圆上,且 ,点 是 上任意一点,连接 、 .则 的度数为
| A. |
|
B. |
|
C. |
|
D. |
|
我们已经接触了很多代数恒等式,知道可以用一些硬纸片拼成的图形面积来解释一些代数恒等式.例如图甲可以用来解释(a+b)2-(a-b)2=4ab.那么通过图乙面积的计算,验证了一个恒等式,此等式是( )

| A.a2-b2=(a+b)(a-b) |
| B.(a-b)(a+2b)=a2+ab-b2 |
| C.(a-b)2=a2-2ab+b2 |
| D.(a+b)2=a2+2ab+b2 |