江苏省镇江市扬中市七年级下学期期末数学试卷
如图,直线l∥m∥n,△ABC的直角顶点B和另一顶点C分别在直线m和n上,边BC与直线n所夹的角∠α为52°,则∠β的度数为 .

某地中学生校园足球联赛,共赛17轮(即每对均需参赛17场),记分办法是:胜1场得3分,平1场得1分,负1场得0分.在这次校园足球联赛中,光明足球队得16分,且踢平场数是所负场数的k倍(k为正整数),则k的所有可能值之和为 .
下列运算中正确的是( ).
| A.(x3)2=x5 | B.2a﹣5•a3=2a8 | C. |
D.6x3÷(﹣3x2)=2x |
如果a>b,c<0,那么下列不等式成立的是( ).
| A.a+c>b+c | B.c﹣a>c﹣b | C.ac>bc | D. |
如图,在△ABC中,BC=5,∠A=80°,∠B=70°,把△ABC沿RS的方向平移到△DEF的位置,若CF=4,则下列结论中错误的是( ).

| A.BE=4 | B.∠F=30° | C.AB∥DE | D.DF=5 |
(﹣x+y)( )=x2﹣y2,其中括号内的是( ).
| A.﹣x﹣y | B.﹣x+y | C.x﹣y | D.x+y |
一个n边形的内角和比它的外角和至少大120°,则n的最小值是( ).
| A.4 | B.5 | C.6 | D.7 |
下列命题中,是真命题的有( ).
①同旁内角互补;
②若n<1,则n2﹣1<0;
③如果一个角的两边分别与另一个角的两边分别平行,那么这两个角相等;
④同一平面内,如果直线l1⊥l2,直线l2⊥l3,那么l1∥l3.
| A.0个 | B.1个 | C.2个 | D.3个 |
已知x=2是不等式﹣3(mx﹣3m+2)≤0的解,且x=1不是这个不等式的解,则实数m的取值范围是( ).
| A.m>1 | B.m<2 | C.1<m≤2 | D.1≤m≤2 |
(1)计算:(﹣a)7÷(﹣a)4×(﹣a)3;
(2)利用乘法公式计算:2014×2016﹣20152;
(3)因式分解:x3﹣4x.
在求1+2+22+23+24+25+26的值时,小明发现:从第二个加数起每一个加数都是前一个加数的2倍,于是他设:S=1+2+22+23+24+25+26①然后在①式的两边都乘以2,得:2S=2+22+23+24+25+26+27 ②;②﹣①得2S﹣S=27﹣1,S=27﹣1,即1+2+22+23+24+25+26=27﹣1.
(1)求1+3+32+33+34+35+36的值;
(2)求1+a+a2+a3+…+a2013(a≠0且a≠1)的值.
已知三元一次方程组 .
.
(1)求该方程组的解;
(2)若该方程组的解使ax+2y+z<0成立,求整数a的最大值.
甲、乙两农户是某农业合作社社员,他们今年种植了新型豌豆和土豆,他们生产的农产品由合作社分别以x万元/吨,y万元/吨的价格收购,他们今年种植面积、亩产量与卖出农产品的总收入如下表:
| 种植户 |
豌豆 |
土豆 |
卖出两种农产品总收入(万元) |
||
| 种植面积(亩) |
每亩产量(吨) |
种植面积(亩) |
每亩产量(吨) |
||
| 甲 |
4 |
1 |
4 |
3 |
4.8 |
| 乙 |
8 |
1 |
2 |
2.5 |
5.8 |
(1)求x、y的值;
(2)为了以进一步调动农户的种植热情,合作社计划明年收购价不变的情况下对种植这两种农产品给予补贴,补贴标准如下:种植豌豆每亩补贴0.06万元,种植土豆每亩补贴0.05万元,甲种植户计划租30亩地用来种植豌豆和土豆,合作社要求豌豆的种植面积低于土豆的种植面积(两种产品的种植面积均为整数亩),每亩产量均保持不变),为了使甲总收入不低于19.62万元,则他有几种种植方案,并指出哪种种植方案收入最高?
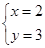 是方程3x﹣my=7的一个解,则m= .
是方程3x﹣my=7的一个解,则m= . x﹣2≥x与不等式3x﹣a≤0解集相同,则a= .
x﹣2≥x与不等式3x﹣a≤0解集相同,则a= .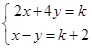 的解x、y之和为2,则k= .
的解x、y之和为2,则k= .
 有解,那么m取值范围为 .
有解,那么m取值范围为 .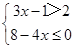 的解集在数轴上表示为( ).
的解集在数轴上表示为( ).



 ;
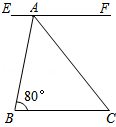
;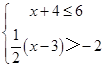 的整数解.
的整数解.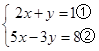 .
.

 粤公网安备 44130202000953号
粤公网安备 44130202000953号