初中数学圆内接四边形的性质试题

已知：如图，在△ABC中，∠BAC=90°,DE、DF是△ABC 的中位线，连接EF、AD，
求证：EF＝AD．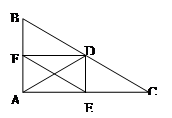

如图，在四边形ABCD中，AB=AD，∠DAB=∠BCD=90°，设p=BC+CD， 四边形ABCD的面积为S．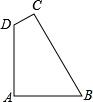

（1）试探究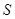与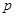之间的关系，并说明理由；
（2）若四边形的面积为9，求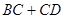的值．

已知：如图①，在Rt△ACB中，∠C=90°，AC="4" cm，BC="3" cm，点P由B出发沿BA方向向点A匀速运动，速度为1cm/s；点Q由A出发沿AC方向向点C匀速运动，速度为2cm/s；连接PQ．若设运动的时间为t（s）（0＜t＜2），解答下列问题：

（1）当t为何值时，PQ∥BC；
（2）设△AQP的面积为y（cm²），求y与t之间的函数关系式；
（3）是否存在某一时刻t，使线段PQ恰好把Rt△ACB的周长和面积同时平分？若存在，求出此时t的值；若不存在，说明理由；
（4）如图②，连接PC，并把△PQC沿QC翻折，得到四边形PQP′C，那么否存在某一时刻t，使四边形PQP′C为菱形？若存在，求出此时菱形的边长；若不存在，说明理由．

（本题满分11分．为方便答题，可在答卷上画出你认为必要的图形）
如图，已知：等腰梯形ABCD中，AD∥BC，AB=CD，E、F、G、H分别是AD、BC、BE、CE的中点．

（1）求证：△ABE≌△DCE；
（2）四边形EGFH是什么特殊四边形？并证明你的结论．
（3）连接EF,当四边形EGFH是正方形时，线段EF与BC有什么数量关系？请说明理由．

如图，在平面直角坐标系中，矩形OCDE的三个顶点分别是C（3，0），D（3，4），E（0，4）．点A在DE上，以A为顶点的抛物线过点C，且对称轴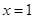交z轴于点B．连接EC，AC．点P，Q为动点，设运动时间为t秒．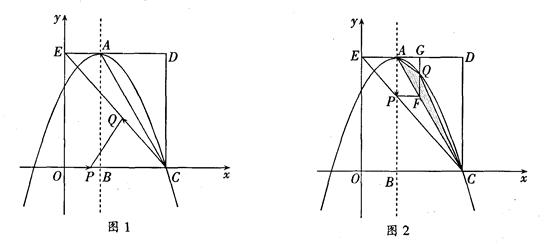

（1）填空：点A坐标为    ，抛物线的解析式为    ；
（2）在图1中，若点P在线段OC上从点O向点C以1个单位／秒的速度运动，同时，点Q在线段CE上从点C向E以2个单位／秒的速度运动，当一个点到达终点时，另一个点随之停止运动．连接PQ，是否存在实数t，使得PQ所在的直线经过点D，若存在，求出t的值；若不存在，请说明理由；
（3）在图2中，若点P在对称轴上从点A开始向点B以1个单位／秒的速度运动，过点P做PF⊥AB，交AC于点F，过点F作FG⊥AD于点G，交抛物线于点Q，连接AQ，CQ．当t为何值时，△ACQ的面积最大？最大值是多少？

如图，已知正比例函数和反比例函数的图象交于点A（m，-2）．

（1）求反比例函数的解析式；
（2）观察图象，直接写出正比例函数值大于反比例函数值时自变量x的取值范围；
（3）若双曲线上点C（2，n）沿OA方向平移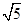个单位长度得到点B，判断四边形OABC的形状并证明你的结论．

已知在矩形中，是边上的一动点，联结、，过点作射线交线段的延长线于点，交边于点，且使得，如果，，，；

（1）求关于的函数解析式，并写出它的定义域；
（2）当时，求的正切值；
（3）如果△是以为底角的等腰三角形，求的长；

已知：如图，在直角梯形ABCD中，AD∥BC，∠B=90°，AD=2，BC=6，AB=3．E为BC边上一点，以BE为边作正方形BEFG，使正方形BEFG和梯形ABCD在BC的同侧．

（1）当正方形的顶点F恰好落在对角线AC上时，求BE的长；
（2）将（1）问中的正方形BEFG沿BC向右平移，记平移中的正方形BEFC为正方形B′EFG，当点E与点C重合时停止平移．设平移的距离为t，正方形B′EFG的边EF与AC交于点M，连接B′D，B′M，DM，是否存在这样的t，使△B′DM是直角三角形？若存在，求出t的值；若不存在，请说明理由．

如图，折叠矩形ABCD的一边AD使点D落在BC边上的E处，已知折痕AF＝10cm，且tan∠FEC＝.

(1)求矩形ABCD的面积；
(2)利用尺规作图求作与四边形AEFD各边都相切的⊙O的圆心O（只须保留作图痕迹），并求出⊙O的半径．

在平面直角坐标系中，正方形ABCD的位置如右图所示，点A的坐标为（1，0），点D的坐标为（0，2），延长CB交x轴于点A₁，作正方形A₁B₁C₁C，延长C₁B₁交x轴于点A₂，作正方形A₂B₂C₂C₁，…按这样的规律进行下去，第1个正方形的面积为            ；第n个正方形的面积为            ．

一块直角三角形木板的一条直角边 AB 的长为1.5米,面积为1.5米 ² ,要把它加工成一个面积最大的正方形桌面,甲、乙两位同学的加工方法分别如图所示,请你用所学的知识说明哪位同学的加工方法符合要求(加工损耗忽略不计,计算结果中的分数可保留).

如图，在△ABD中，AB=AD,AO平分∠BAD,过点D作AB的平行线交AO的延长线于点C,连接BC

（1）求证：四边形ABCD是菱形。
（2）如果OA,OB(OA>OB)的长（单位：米）是一元二次方程的两根，求AB的长以及菱形ABCD的面积。
（3）若动点M从A出发，沿AC以2m/S的速度匀速直线运动到点C,动点N从B 出发，沿BD以1m/S的速度匀速直线运动到点D，当M运动到C点时运动停止。若M、N同时出发，问出发几秒钟后，△MON的面积为？

如图，正方形ABCD的边长为1，点E是AD边上的动点，从点A沿AD向D运动，以BE为边，在BE的上方作正方形BEFG，连接CG．请探究：

（1）线段AE与CG是否相等？请说明理由．
（2）若设，，当取何值时，最大？
（3）连接BH，当点E运动到AD的何位置时，△BEH∽△BAE？

已知两个连体的正方形（有两条边在同一条直线上）在正方形网格上的位置如图所示，请你把它分割后，拼接成一个新的正方形. （要求：在正方形网格图中用实线画出拼接成的新正方形且新正方形的顶点在网格的格点上，不写作法）.

如图1，在平面内选一定点O，引一条有方向的射线Ox，再选定一个单位长度，那么平面上任一点M的位置可由∠MOx的度数θ与OM的长度m确定，有序数对（θ，m）称为M点的“极坐标”，这样建立的坐标系称为“极坐标系”．在图2的极坐标系下，如果正六边形的边长为2，有一边OA在射线Ox上，则正六边形的顶点C的极坐标应记为（  ）

A．（60°，4）

B．（45°，4）

C．（60°，）

D．（50°，）