上海市四区联考九年级一模数学试卷
如果把 的三边长度都扩大2倍,那么锐角
的三边长度都扩大2倍,那么锐角 的四个三角比的值( )
的四个三角比的值( )
| A.都扩大到原来的2倍; | B.都缩小到原来的 ; ; |
| C.都没有变化; | D.都不能确定; |
一个小球被抛出后,如果距离地面的高度 (米)和运行时间
(米)和运行时间 (秒)的函数解析式为
(秒)的函数解析式为 ,那么小球到达最高点时距离地面的高度是( )
,那么小球到达最高点时距离地面的高度是( )
| A.1米; | B.3米; | C.5米; | D.6米; |
如图,已知在梯形 中,
中, ∥
∥ ,
, ,如果对角线
,如果对角线 与
与 相交于点
相交于点 ,
,
△ 、△
、△ 、△
、△ 、△
、△ 的面积分别记作
的面积分别记作 、
、 、
、 、
、 ,那么下列结论中,不正确的
,那么下列结论中,不正确的
是( )
A. ; ; |
B. ; ; |
C. ; ; |
D. ; ; |
已知不等臂跷跷板 长为3米,当
长为3米,当 的一端点
的一端点 碰到地面时(如图1),
碰到地面时(如图1), 与地面的夹角
与地面的夹角
为30°;当 的另一端点
的另一端点 碰到地面时(如图2),
碰到地面时(如图2), 与地面的夹角的正弦值为
与地面的夹角的正弦值为 ,那么跷跷板
,那么跷跷板 的
的
支撑点 到地面的距离
到地面的距离 米
米

把一个三角形绕其中一个顶点逆时针旋转并放大或缩小(这个顶点不变),我们把这样的三角形
运动称为三角形的T-变换,这个顶点称为T-变换中心,旋转角称为T-变换角,三角形与原三角形的对应边
之比称为T-变换比;已知△ 在直角坐标平面内,点
在直角坐标平面内,点 ,
, ,
, ,将△
,将△ 进
进
行T-变换,T-变换中心为点 ,T-变换角为60°,T-变换比为
,T-变换角为60°,T-变换比为 ,那么经过T-变换后点
,那么经过T-变换后点 所对应的点的
所对应的点的
坐标为 ;
已知在直角坐标平面内,抛物线 经过
经过 轴上两点
轴上两点 ,点
,点 的坐标为
的坐标为 ,与
,与 轴相交于点
轴相交于点 ;
;
(1)求抛物线的表达式;
(2)求△ 的面积;
的面积;
如图,已知在△ 中,
中, 是边
是边 上的中线,设
上的中线,设 ,
, ;
;
(1)求 (用向量
(用向量 的式子表示)
的式子表示)
(2)如果点 在中线
在中线 上,求作
上,求作 在
在 方向上的分向量;(不要求写作法,但要保留作图痕迹,并指出所作图中表示结论的分向量)
方向上的分向量;(不要求写作法,但要保留作图痕迹,并指出所作图中表示结论的分向量)
如图,某幢大楼的外墙边上竖直安装着一根旗杆 ,小明在离旗杆下方大楼底部
,小明在离旗杆下方大楼底部 点24米的点
点24米的点 处放置一台测角仪,测角仪的高度
处放置一台测角仪,测角仪的高度 为1.5米,并在点
为1.5米,并在点 处测得旗杆下端
处测得旗杆下端 的仰角为40°,上端
的仰角为40°,上端 的仰角为45°,求旗杆
的仰角为45°,求旗杆 的长度;(结果精确到0.1米,参考数据:
的长度;(结果精确到0.1米,参考数据: ,
, ,
, )
)
用含30°、45°、60°这三个特殊角的四个三角比及其组合可以表示某些实数,如:
可表示为 ;仿照上述材料,完成下列问题:
;仿照上述材料,完成下列问题:
(1)用含30°、45°、60°这三个特殊角的三角比或其组合表示 ,即填空:
,即填空:


 …;
…;
(2)用含30°、45°、60°这三个特殊角的三角比,结合加、减、乘、除四种运算,设计一个等式,要求:等式中须含有这三个特殊角的三角比,上述四种运算都至少出现一次,且这个等式的结果等于1,即填空:
已知在平面直角坐标系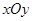 中,二次函数
中,二次函数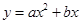 的图像经过点
的图像经过点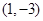 和点
和点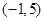 ;
;
(1)求这个二次函数的解析式;
(2)将这个二次函数的图像向上平移,交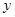 轴于点
轴于点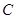 ,其纵坐标为
,其纵坐标为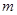 ,请用
,请用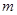 的代数式表示平移后函数图象顶点
的代数式表示平移后函数图象顶点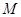 的坐标;
的坐标;
(3)在第(2)小题的条件下,如果点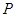 的坐标为
的坐标为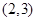 ,
,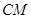 平分
平分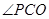 ,求
,求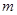 的值;
的值;
 向左平移2个单位,所得抛物线的表达式为( )
向左平移2个单位,所得抛物线的表达式为( ) ;
; ;
; ;
; ;
; ∥
∥ ∥
∥ ,
, ,
, ,那么
,那么 的长等于( )
的长等于( )
 ;
; ;
; 中,
中, ,
, ,那么边
,那么边 的长等于( )
的长等于( ) ;
; ;
; ;
; ;
; ,那么
,那么 ;
; ;
; ,
, ,那么线段
,那么线段 、
、 的比例中项等于
的比例中项等于 
 的图像与
的图像与 轴的交点坐标为 ;
轴的交点坐标为 ; 中,
中, ,如果
,如果 ,
, ,那么
,那么 ;
; 分别是△
分别是△ 的边
的边 和
和 上的点,
上的点, ,
, ,要使
,要使 ∥
∥ ,
, 应等于 ;
应等于 ;
 不经过第一象限,那么
不经过第一象限,那么 的取值范围是 ;
的取值范围是 ; 是面积为
是面积为 的△
的△ 的重心,那么△
的重心,那么△ 的面积等于 ;
的面积等于 ; 的坡面由
的坡面由 到
到 直行走了26米时,小杰实际上升的高度
直行走了26米时,小杰实际上升的高度

 ,对称轴为直线
,对称轴为直线 ,由此可知这个二次函数的图像一定
,由此可知这个二次函数的图像一定 是△
是△ 的边
的边 上一点,
上一点, ∥
∥ ,交边
,交边 于点
于点 ,延长
,延长 ,使
,使 ,联结
,联结 ,交边
,交边 ,联结
,联结

 ;
; ,求证:
,求证:
 中,
中, 是边
是边 上的一动点,联结
上的一动点,联结 、
、 ,过点
,过点 作射线交线段
作射线交线段 ,交边
,交边 ,且使得
,且使得 ,如果
,如果 ,
, ,
, ,
, ;
;
 关于
关于 的函数解析式,并写出它的定义域;
的函数解析式,并写出它的定义域; 时,求
时,求 的正切值;
的正切值; 是以
是以 为底角的等腰三角形,求
为底角的等腰三角形,求 的长;
的长; 粤公网安备 44130202000953号
粤公网安备 44130202000953号