如图, 为 的直径, , 为 上两点,若 ,则 的大小为
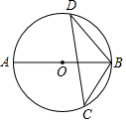
| A. |
|
B. |
|
C. |
|
D. |
|
图中有两张型号完全一样的折叠式饭桌,将正方形桌面边上的四个弓形面板翻折起来后,就能形成一个圆形桌面(可近似看作正方形的外接圆),正方形桌面与翻折成的圆形桌面的面积之比最接近

| A. |
|
B. |
|
C. |
|
D. |
|
如图,抛物线过点
,且与直线
交于
、
两点,点
的坐标为
.

(1)求抛物线的解析式;
(2)点为抛物线上位于直线
上方的一点,过点
作
轴交直线
于点
,点
为对称轴上一动点,当线段
的长度最大时,求
的最小值;
(3)设点为抛物线的顶点,在
轴上是否存在点
,使
?若存在,求点
的坐标;若不存在,请说明理由.
如图,线段经过
的圆心
,交
于
、
两点,
,
为
的弦,连结
,
,连结
并延长交
于点
,连结
交
于点
.
(1)求证:直线是
的切线;
(2)求的半径
的长;
(3)求线段的长.
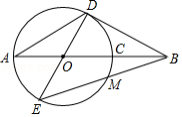
如图,已知是
的直径,
,
是
的弦,
交
于
,过点
作
的切线交
的延长线于点
,连接
并延长交
的延长线于点
.
(1)求证:是
的切线;
(2)若,
,求线段
的长.

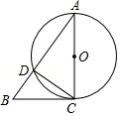
如图,内接于
,直径
交
于点
,延长
至点
,使
,连接
并延长交过点
的切线于点
,且满足
,连接
,若
,
.
(1)求证:;
(2)求的半径
;
(3)求证:是
的切线.

如图,在中,以
为直径的
交
于点
,连接
,
.
(1)求证:是
的切线;
(2)若,
,求点
到
的距离.
如图,在以点为中心的正方形
中,
,连接
,动点
从点
出发沿
以每秒1个单位长度的速度匀速运动,到达点
停止.在运动过程中,
的外接圆交
于点
,连接
交
于点
,连接
,将
沿
翻折,得到
.
(1)求证:是等腰直角三角形;
(2)当点恰好落在线段
上时,求
的长;
(3)设点运动的时间为
秒,
的面积为
,求
关于时间
的关系式.

如图,是
的直径,点
为
的中点,
为
的弦,且
,垂足为
,连接
交
于点
,连接
,
,
.
(1)求证:;
(2)若,求
的长.

如图, 的直径 垂直于弦 ,垂足是点 , , ,则 的长为
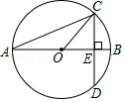
| A. |
|
B. |
|
C. |
6 |
D. |
12 |
如图,为
的直径,点
在
的延长线上,点
在
上,且
.
(1)求证:是
的切线;
(2)已知,
,点
是
的中点,
,垂足为
,
交
于点
,求
的长.
