(·辽宁朝阳)某农场急需铵肥8吨,在该农场南北方向分别有一家化肥公司A、B,A公司有铵肥3吨,每吨售价750元;B公司有铵肥7吨,每吨售价700元,汽车每千米的运输费用b(单位:元/千米)与运输重量a(单位:吨)的关系如图所示.
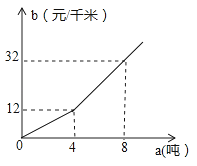
(1)根据图象求出b关于a的函数解析式(包括自变量的取值范围);
(2)若农场到B公司的路程是农场到A公司路程的2倍,农场到A公司的路程为m千米,设农场从A公司购买x吨铵肥,购买8吨铵肥的总费用为y元(总费用=购买铵肥费用+运输费用),求出y关于x的函数解析式(m为常数),并向农场建议总费用最低的购买方案.