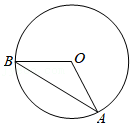
如图, 是 的直径,弦 ,垂足为点 ,连接 , .如果 , ,那么图中阴影部分的面积是

A. B. C. D.
如图, 是半圆 的直径, 是半圆上的一点, 平分 交半圆于点 ,过点 作 与 的延长线交于点 .
(1)求证: 是半圆的切线;
(2)若 , ,求半圆的直径.

如图,已知 的直径 ,弦 , 的平分线交 于点 ,过点 作 交 的延长线于点 .
(1)求证: 是 的切线.
(2)求 的长.

一次函数 的图象与 轴的负半轴相交于点 ,与 轴的正半轴相交于点 ,且 . 的外接圆的圆心 的横坐标为 .
(1)求一次函数的解析式;
(2)求图中阴影部分的面积.

如图,公园内有一个半径为18米的圆形草坪,从 A地走到 B地有观赏路(劣弧 AB)和便民路(线段 AB).已知 A、 B是圆上的点, O为圆心, ,小强从 A走到 B,走便民路比走观赏路少走( )米.
| A. |
|
B. |
|
C. |
|
D. |
|
如图,在 中, , , ,以边 上一点 为圆心, 为半径的 经过点 .
(1)求 的半径;
(2)点 为劣弧 中点,作 ,垂足为 ,求 的长;
(3)在(2)的条件下,连接 ,求 的值.
已知:如图,在 中, ,点 是底边 上一点且满足 , 是 的外接圆,过点 作 交 于点 .
(1)求证: 是 的切线;
(2)若 , ,求 的半径.

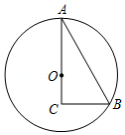
如图, 的半径 垂直于弦 ,垂足为点 ,连接 并延长交 于点 ,连接 , .若 , ,则 的面积为

A.12B.15C.16D.18
如图, 是 的直径,弦 于点 ,连结 , .若 的半径为 , ,则下列结论一定成立的是
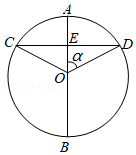
| A. |
|
B. |
|
| C. |
|
D. |
|
如图, 为 的直径,弦 于点 , 于点 ,若 , ,则 的长度是
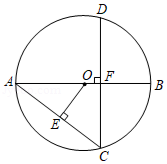
| A. |
9.6 |
B. |
|
C. |
|
D. |
10 |
如图,在菱形 中,对角线 、 相交于点 , 经过点 , ,交对角线 于点 ,且 ,连接 交 于点 .
(1)试判断 与 的位置关系,并说明理由;
(2)若 , ,求 的半径.
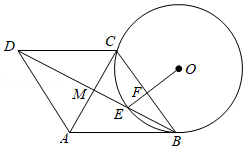
如图,在 中, 为 的直径, 为 上一点, 是 的中点,过点 作 的垂线,交 的延长线于点 ,连接 .
(1)求证: 是 的切线;
(2)若 , ,求 的长.
