如图，在长方形ABCD中，，AB=6cm，BC=8cm，按图中所示方法将△BCD沿BD折叠，使点C落在点E处，BE交AD于点F，
求证：△FBD是等腰三角形；
求AF长。
请阅读下列材料：
问题：如图①，将菱形ABCD和菱形BEFG拼接在一起，使得点A，B，E在同一条直线上，点G在BC边上，P是线段DF的中点，连接PG，PC．若∠ABC=120°，试探究PG与PC的位置关系及∠PCG的大小．小明同学的思路是：延长GP交DC于点H，构造全等三角形，经过推理使问题得到解决．请你参考小明的思路，探究并解决下列问题：
（1）直接写出上面问题中线段PG与PC的位置关系及∠PCG的大小；
（2）将图①中的菱形BEFG绕点B顺时针旋转，使点E恰好落在CB的延长线上，原问题中的其他条件不变（如图②）．你在（1）中得到的两个结论是否仍成立？写出你的猜想并加以证明．
如图，在矩形ABCD中，AB=3cm，AD=4cm，点E是BC上一动点（不与B、C重合），且DF⊥AE，垂足为F. 设AE=xcm，DF=ycm.（1）求证：△DFA∽△ABE；
（2）试求y与x之间的函数关系式，并求出自变量的取值范围.
(本题满分10分)
如图，若∠AOB=∠ACB=90°，OC平分∠AOB.
你能将四边形AOBC通过剪裁拼成一个正方形吗？画出裁剪方法并有必要的说明。
②、若OC=2，你能求出四边形AOBC的面积吗？
如图，在梯形ABCD中，AD∥BC，AB=AD+BC，E为CD的中点.
求证：AE⊥BE.
如图，四边形ABCD是菱形，DE⊥AB交BA的延长线于点E，DF⊥BC交BC的延长线于点F。请你猜想DE与DF的什么关系，证明你的猜想。
如图所示，在菱形ABCD中，AB=4，∠BAD=120°，△AEF为正三角形，点E、F分别在菱形的边BC、CD上滑动，且E、F不与B、C、D重合．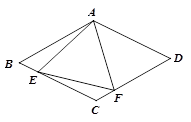
（1）证明不论E、F在BC．CD上如何滑动，总有BE=CF；
（2）当点E、F在BC．CD上滑动时，分别探讨四边形AECF的面积和△CEF的周长是否发生变化？如果不变，求出这个定值；如果变化，求出最小值．
我们把两条中线互相垂直的三角形称为“中垂三角形”．例如图1，图2，图3中，AF，BE是△ABC的中线， AF⊥BE ， 垂足为P．像△ABC这样的三角形均为“中垂三角形”．设
，
，
．
特例探索
（1）如图1，当∠
=45°，
时，= ，
；
如图2，当∠=30°，
时， = ， ；
归纳证明
（2）请你观察（1）中的计算结果，猜想
三者之间的关系，用等式表示出来，并利用图3证明你发现的关系式；
拓展应用
（3）如图4，在□ABCD中，点E，F，G分别是AD，BC，CD的中点，BE⊥EG， AD= 
，AB=3．求AF的长．
如图，在直角梯形ABCD中，AD∥BC，∠B=90°，且AD=12cm，AB=8cm，DC=10cm，若动点P从A点出发，以每秒2cm的速度沿线段AD向点D运动；动点Q从C点出发以每秒3cm的速度沿CB向B点运动，当P点到达D点时，动点P、Q同时停止运动，设点P、Q同时出发，并运动了t秒，回答下列问题：
（1）BC= cm；
（2）当t为多少时，四边形PQCD成为平行四边形？
（3）当t为多少时，四边形PQCD为等腰梯形？
（4）是否存在t，使得△DQC是等腰三角形？若存在，请求出t的值；若不存在，说明理由．
已知▱ABCD中，AE平分∠BAD，CF平分∠BCD，分别交CD、AB于E、F，求证：AE=CF．
△ABC中，AB=AC=10，BC=12，矩形DEFG中，EF=4，FG＞12．
（1）如图①，点A是FG的中点，FG∥BC，将矩形DEFG向下平移，直到DE与BC重合为止．要研究矩形DEFG与△ABC重叠部分的面积，就要进行分类讨论，你认为如何进行分类，写出你的分类方法（无需求重叠部分的面积）．
（2）如图②，点B与F重合，E、B．C在同一直线上，将矩形DEFG向右平移，直到点E与C重合为止．设矩形DEFG与△ABC重叠部分的面积为y，平移的距离为x．
①求y与x的函数关系式，并写出自变量的取值范围；
②在给定的平面直角坐标系中画出y与x的大致图象，并在图象上标注出关键点坐标．
如图1，在△ABC中，AB＝BC＝5，AC="6." △ECD是△ABC沿BC方向平移得到的，连接AE. AC和BE相交于点O.
ABCD的两条对角线线交于O，且
。
粤公网安备 44130202000953号