初中数学圆解答题

在一张桌子的桌面长为6m，宽为4m，台布面积是桌面面积的2倍，如果将台布铺在桌子上，各边垂下的长度相同，求这块台布的长和宽？

如图，四边形ABCD是长方形.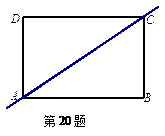

（1）作△ABC关于直线AC对称的图形；
（2）试判断（1）中所作的图形与△ACD重叠部分的三角形形状，并说明理由.

(12分)
已知在菱形ABCD中，E是BC的中点，且∠FAE=∠BAE．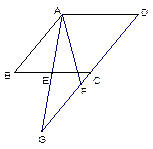

(1) 如图，当点F在边DC的延长线上时，求证：AF=BC－CF；
(2) 当点F与点C重合时，求∠B的度数，并说明理由；
(3) 当点F在边DC上时，（1）中求证的结论还成立吗？若不成立，
请直接写出成立的结论；
(4)当∠B=90°时，请确定点F的位置

如图2，梯形ABCD中，AB∥CD，且AB＝2CD，E、F分别是AB、BC的中点，EF与BD相交于点M。

⑴求证：△EDM∽△FBM
⑵若DB＝9，求BM的长

（本题10分）如图4，边长为的矩形，它的周长为14，面积为10，求下列各式的值：(1)   (2)

图4

 

本题10分）
（1）拼一拼，画一画：请你用4个长为a，宽为b的矩形拼成一个大正方形，并且正中间留下一个洞，这个洞恰好是一个小正方形。
（2）用不同方法计算中间的小正方形的面积，聪明的你能发现什么？
（3）当拼成的这个大正方形边长比中间小正方形边长多3cm时，它的面积就多24cm2，求中间小正方形的边长。

如图11-①，为的直径，与相切于点与相切于点，点为延长线上一点，且

（1）求证：为的切线；
（2）连接，的延长线与的延长线交于点（如图11-②所示）.若，求线段和的长.

在梯形ABCD中，AD//BC,AB=CD,E为AD中点

（1）求证：△ABE≌△DCE
（2）若BE平分,且AD=10,求AB的长

（本小题满分12分）
如图16，在直角梯形ABCD中，AD∥BC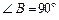，，AD = 6，BC = 8，，点M是BC的中点．点P从点M出发沿MB以每秒1个单位长的速度向点B匀速运动，到达点B后立刻以原速度沿BM返回；点Q从点M出发以每秒1个单位长的速度在射线MC上匀速运动．在点P，Q的运动过程中，以PQ为边作等边三角形EPQ，使它与梯形ABCD在射线BC的同侧．点P，Q同时出发，当点P返回到点M时停止运动，点Q也随之停止．
设点P，Q运动的时间是t秒(t＞0)．

（1）设PQ的长为y，在点P从点M向点B运动的过程中，写出y与t之间的函数关系式（不必写t的取值范围）．
（2）当BP = 1时，求△EPQ与梯形ABCD重叠部分的面积．
（3）随着时间t的变化，线段AD会有一部分被△EPQ覆盖，被覆盖线段的长度在某个时刻会达到最大值，请回答：该最大值能否持续一个时段？若能，直接写出t的取值范围；若不能，请说明理由．

（本小题满分8分）如图11-1，正方形ABCD是一个6 × 6网格电子屏的示意图，其中每个小正方形的边长为1．位于AD中点处的光点P按图11-2的程序移动．

（1）请在图11-1中画出光点P经过的路径；
（2）求光点P经过的路径总长（结果保留π）．