如图,在矩形 中, , ,点 为线段 上的动点,将 沿 折叠,使点 落在矩形内点 处,下列结论正确的是 (写出所有正确结论的序号)
①当 为线段 中点时, ;
②当 为线段 中点时, ;
③当 、 、 三点共线时, ;
④当 、 、 三点共线时, .

如图,在矩形 中, , ,矩形内部有一动点 满足 ,则点 到 、 两点的距离之和 的最小值为 .

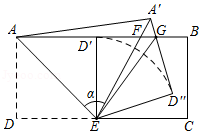
如图,在矩形 中, , .把 沿 折叠,使点 恰好落在 边上的 处,再将 绕点 顺时针旋转 ,得到△ ,使得 恰好经过 的中点 . 交 于点 ,连接 .有如下结论:① 的长度是 ;②弧 的长度是 ;③△ △ ;④△ .上述结论中,所有正确的序号是 .
如图,在河对岸有一矩形场地 ,为了估测场地大小,在笔直的河岸 上依次取点 , , ,使 , ,点 , , 在同一直线上.在 点观测 点后,沿 方向走到 点,观测 点发现 .测得 米, 米, 米, ,则场地的边 为 米, 为 米.

如图,在矩形 中, ,将矩形 绕点 逆时针旋转,得到矩形 ,点 的对应点 落在 上,且 ,则 的长为 .

图1是一种矩形时钟,图2是时钟示意图,时钟数字2的刻度在矩形 的对角线 上,时钟中心在矩形 对角线的交点 上.若 ,则 长为 (结果保留根号).
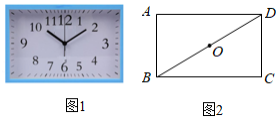
如图,在矩形 中, , ,点 在 上, ,点 是边 上一动点,以 为斜边作 .若点 在矩形 的边上,且这样的直角三角形恰好有两个,则 的值是 .

如图,在平面直角坐标系 中,有一个由六个边长为1的正方形组成的图案,其中点 , 的坐标分别为 , .若过原点的直线 将这个图案分成面积相等的两部分,则直线 的函数解析式为 .
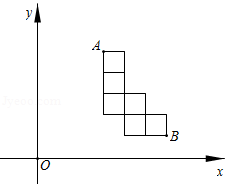
如图,在矩形 中,按以下步骤作图:①分别以点 和 为圆心,以大于 的长为半径作弧,两弧相交于点 和 ;②作直线 交 于点 .若 , ,则矩形的对角线 的长为 .

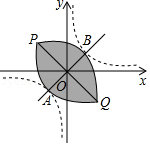
设双曲线 与直线 交于 , 两点(点 在第三象限),将双曲线在第一象限的一支沿射线 的方向平移,使其经过点 ,将双曲线在第三象限的一支沿射线 的方向平移,使其经过点 ,平移后的两条曲线相交于 , 两点,此时我们称平移后的两条曲线所围部分(如图中阴影部分)为双曲线的“眸”, 为双曲线的“眸径“,当双曲线 的眸径为6时, 的值为 .
如图,平面直角坐标系中,矩形 的顶点 , , .将矩形 绕点 顺时针方向旋转,使点 恰好落在 上的点 处,则点 的对应点 的坐标为 .

如图,矩形 的对角线 , 交于点 ,分别以点 , 为圆心, 长为半径画弧,分别交 , 于点 , .若 , ,则图中阴影部分的面积为 .(结果保留
点 , , 在反比例函数 (常数 , 图象上的位置如图所示,分别过这三个点作 轴、 轴的平行线.图中所构成的阴影部分面积从左到右依次为 , , .若 , ,则 的值为 .
