将一张三角形纸片按如图步骤①至④折叠两次得图⑤,然后剪出图⑤中的阴影部分,则阴影部分展开铺平后的图形是

| A. |
等腰三角形 |
B. |
直角三角形 |
C. |
矩形 |
D. |
菱形 |
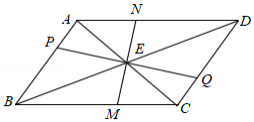
如图,在矩形 中, , 相交于点 ,过点 作 于点 ,交 于点 ,过点 作 交 于点 .交 于点 ,连接 , .有下列结论:①四边形 为平行四边形;② ;③ 为等边三角形;④当 时,四边形 是菱形.其中,正确结论的序号 .

如图,在 中,对角线 与 相交于点 ,过点 的直线 与 、 的延长线分别交于点 、 .
(1)求证: ;
(2)请再添加一个条件,使四边形 是菱形,并说明理由.

如图, 是边长为1的等边三角形, 、 为线段 上两动点,且 ,过点 、 分别作 、 的平行线相交于点 ,分别交 、 于点 、 .现有以下结论: ;②当点 与点 重合时, ;③ ;④当 时,四边形 为菱形,其中正确结论为
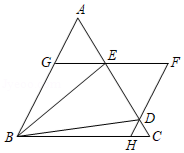
| A. |
①②③ |
B. |
①②④ |
C. |
①②③④ |
D. |
②③④ |
如图, 是 的对角线.
(1)尺规作图(请用 铅笔):作线段 的垂直平分线 ,交 , , 分别于 , , ,连接 , (保留作图痕迹,不写作法).
(2)试判断四边形 的形状并说明理由.

如图, 、 、 分别是 各边的中点,连接 、 、 .
(1)求证:四边形 为平行四边形;
(2)加上条件 后,能使得四边形 为菱形,请从① ;② 平分 ;③ 这三个条件中选择1个条件填空(写序号),并加以证明.

如图, 、 、 分别是 各边中点,则以下说法错误的是

| A. |
和 的面积相等 |
| B. |
四边形 是平行四边形 |
| C. |
若 ,则四边形 是菱形 |
| D. |
若 ,则四边形 是矩形 |
如图①,在 中, , , 是斜边 上的中线,点 为射线 上一点,将 沿 折叠,点 的对应点为点 .

(1)若 .直接写出 的长(用含 的代数式表示);
(2)若 ,垂足为 ,点 与点 在直线 的异侧,连接 ,如②,判断四边形 的形状,并说明理由;
(3)若 ,直接写出 的度数.
如图,在矩形 中,对角线 与 相交于点 , ,对角线 所在的直线绕点 顺时针旋转角 ,所得的直线 分别交 , 于点 , .
(1)求证: ;
(2)当旋转角 为多少度时,四边形 为菱形?试说明理由.

如图, 为 的对角线.
(1)作对角线 的垂直平分线,分别交 , , 于点 , , (尺规作图,不写作法,保留作图痕迹);
(2)连接 , ,求证:四边形 为菱形.

如图,在矩形 中,点 , 分别在 , 上, .只需添加一个条件即可证明四边形 是菱形,这个条件可以是 (写出一个即可).

如图,矩形 中, , 相交于点 ,过点 作 交 于点 ,交 于点 ,过点 作 交 于点 ,交 于点 ,连接 , .则下列结论:
① ;
② ;
③ ;
④当 时,四边形 是菱形.
其中,正确结论的个数是

| A. |
1个 |
B. |
2个 |
C. |
3个 |
D. |
4个 |
如图,过 对角线 与 的交点 作两条互相垂直的直线,分别交边 、 、 、 于点 、 、 、 .
(1)求证: ;
(2)顺次连接点 、 、 、 ,求证:四边形 是菱形.