如图,在菱形 中, , , 分别在边 , 上,将四边形 沿 翻折,使 的对应线段 经过顶点 ,当 时, 的值为 .

如图所示,四边形 是菱形,边 在 轴上,点 ,点 ,双曲线 与直线 交于点 、点 .
(1)求 的值;
(2)求直线 的解析式;
(3)求 的面积.
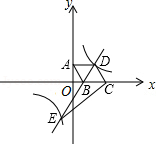
如图,在平面直角坐标系中,坐标原点 是菱形 的对称中心.边 与 轴平行,点 ,反比例函数 的图象经过 , 两点.
(1)求点 的坐标及反比例函数的解析式.
(2)直线 与反比例函数图象的另一交点为 ,求以 , , 为顶点的三角形的面积.

对角线长分别为6和8的菱形 如图所示,点 为对角线的交点,过点 折叠菱形,使 , 两点重合, 是折痕.若 ,则 的长为

A.7B.6C.5D.4
如图,菱形 的边长是4厘米, ,动点 以1厘米秒的速度自 点出发沿 方向运动至 点停止,动点 以2厘米 秒的速度自 点出发沿折线 运动至 点停止.若点 、 同时出发运动了 秒,记 的面积为 厘米 ,下面图象中能表示 与 之间的函数关系的是
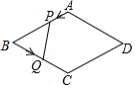
A.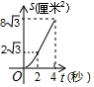 B.
B.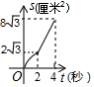
C.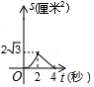 D.
D.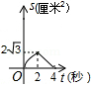
如图,菱形 的对角线 , 相交于点 , , ,则菱形 的周长为

A.52B.48C.40D.20
图①、图②都是由边长为1的小菱形构成的网格,每个小菱形的顶点称为格点.点 , , , , 均在格点上,请仅用无刻度直尺在网格中完成下列画图.
(1)在图①中,画出 的平分线 ;
(2)在图②中,画一个 ,使点 在格点上.

如图,在平面直角坐标系 中,菱形 的边长为2,点 在第一象限,点 在 轴正半轴上, ,若将菱形 绕点 顺时针旋转 ,得到四边形 ,则点 的对应点 的坐标为 .

菱形不具备的性质是
A.四条边都相等B.对角线一定相等
C.是轴对称图形D.是中心对称图形
如图,在平面直角坐标系 中,函数 的图象经过菱形 的顶点 和边 的中点 ,若菱形 的边长为3,则 的值为 .

如图,在直角坐标系 中,菱形 的边 在 轴正半轴上,点 , 在第一象限, ,边长 .点 从原点 出发沿 轴正半轴以每秒1个单位长的速度作匀速运动,点 从 出发沿边 以每秒2个单位长的速度作匀速运动,过点 作直线 垂直于 轴并交折线 于 ,交对角线 于 ,点 和点 同时出发,分别沿各自路线运动,点 运动到原点 时, 和 两点同时停止运动.
(1)当 时,求线段 的长;
(2)求 为何值时,点 与 重合;
(3)设 的面积为 ,求 与 的函数关系式及 的取值范围.
